0087

89

$ 1. Definicja i warunki istnienia całki oznaczonej

ponieważ zaś ostatnia suma dąży do zera (przy A -* 0), więc pierwsza również dąży do zera, a stąd wynika już całkowalność funkcji |/(x)|.

II. Jeśli funkcje f (x) i g(x) są całkowalne w przedziale <a, by, to suma, różnica i iloczyn tych funkcji są także całkowalne.

Dowód ograniczamy do przypadku iloczynu f(x)g(x).

Niech będzie |/(x)| < K, \g (x)| < L. Wybierzmy w przedziale <.x_t,x_l+1y dowolne punkty x', x" i rozpatrzmy różnicę

Hx")g(x")-f(x') g (x ) = [/(x")-/(x')] g(x")+l9 (*")-£ (*')]/(*') •

Jeśli przez o>_t, 0)_t oznaczymy odpowiednio oscylacje funkcji f(x) i g(x) w przedziale to otrzymamy

|/(x") g (x")-/(*') 9 (*')l < Lco_t-Km_t.

Ale wtedy [85] również i dla oscylacji S2₍ funkcji/(x) g(x) w tym przedziale będziemy mieli nierówność

Di < Lco,+Kcoi.

skąd

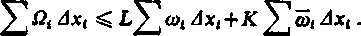
Ponieważ obie sumy dążą do zera (gdy A -» 0), więc również pierwsza suma dąży do zera, a to już dowodzi całkowalności funkcji f(x) g (x).

III.    Jeśli funkcja f (x) jest całkowalna w przedziale <a, by, to jest ona również całkowalna w dowolnym podprzedziale <a, /?> tego przedziału. Na odwrót, jeśli przedział (a, by można rozbić na mniejsze przedziały takie, że w każdym z nich funkcja f{x) jest całkowalna, to jest ona również całkowalna w całym przedziale <a, by.

Dowód. Zakładamy, że funkcja/(x) jest całkowalna w przedziale <a, b); utworzymy dla tego przedziału sumę 2co, Ax, (przyjmując, że a i fi należą do punktów podziału). Analogiczną sumę dla przedziału <a, j?> otrzymujemy przez opuszczenie w poprzedniej sumie niektórych (dodatnich) składników; jest ona więc na pewno zbieżna do zera, jeśli tylko zbieżna jest do zera pierwsza suma.

Przypuśćmy teraz, że przedział <«, b} jest rozbity na dwa podprzedziały <a, c> i <c, by (gdzie a < c < ó) i że w każdym z nich funkcja f(x) jest całkowalna. Utwórzmy znowu sumę 2c°t Ax_t odpowiadającą jakiemuś podziałowi przedziału <a, by; jeśli punkt c jest jednym z punktów podziału, to wymieniona suma składa się z dwóch analogicznych sum, utworzonych dla przedziałów <a, c> oraz <c, by i dąży do zera wraz z nimi. Wniosek ten pozostaje w mocy także i w przypadku, kiedy c nie jest punktem podziału: dodając bowiem jeden nowy punkt podziału zmienimy tylko jeden składnik sumy, który sam oczywiście dąży do zera.

IV.    Jeśli zmienimy wartości funkcji całkowalnej w skończonej liczbie (= k) punktów, to otrzymana w ten sposób nowa funkcja będzie nadał całkowalna.

Dowód jest prosty z uwagi na to, że wspomniane zmiany wystąpią co najwyżej w k składnikach sumy J.co_t ńx_t.