0081

83

§ 1. Definicja i warunki istnienia całki oznaczonej

Podstawimy sobie teraz za zadanie znalezienie warunków, przy których suma całkowa <r ma skończoną granicę, tzn. warunków, przy których istnieje całka oznaczona (4).

Zauważymy przede wszystkim, że podana definicja może być zastosowana jedynie dla funkcji ograniczonej. Rzeczywiście, gdyby funkcja f(x) była w przedziale <a, ó> nieograniczona, to w dowolnym podziale tego przedziału na części znaleźlibyśmy przynajmniej jeden taki podprzedział, w którym własność ta byłaby zachowana. Wtedy wybierając odpowiednio w tym podprzedziale punkt f można by sprawić, żeby/(£), a więc i suma a były dowolnie duże; w tych warunkach oczywiście nie może istnieć skończona granica sum <7. A więc funkcja całkowalna jest zawsze ograniczona.

Dlatego też w dalszych rozważaniach będziemy z góry zakładali, że rozpatrywana funkcja f{x) jest ograniczona, tzn. że

m < f{x) < M

dla a < x < b.

296. Sumy Darboux. Jako pomocnicze narzędzie badania, na równi z sumami całkowymi wprowadzimy za przykładem Darbóux jeszcze inne sumy, podobne do nich, chociaż prostsze.

Oznaczmy odpowiednio przez m_t i M_t kresy dolny i górny funkcji /(x) w /-tym przedziale <*,, x₁₊₁> i utwórzmy sumy

n— 1    n—1

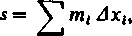
S = ^ Af, Ax,.

i-o    1=0

Sumy te noszą odpowiednio nazwy dolnej i górnej sumy całkowej, lub krótko sum Darboux.

W szczególnym przypadku, kiedy funkcja /(*) jest ciągła, są one po prostu równe najmniejszej i największej z sum całkowych odpowiadających danemu podziałowi rozpatrywanego przedziału, ponieważ w tym przypadku funkcja / (x) osiąga w każdym przedziale swój kres dolny i górny, a więc punkty f, można wybrać tak, żeby było

/(£<) = m, lub /(fj) = M,.

W przypadku ogólnym mamy wprost z definicji kresów dolnego i górnego

m_t    <M,.

Mnożąc stronami obie te nierówności przez Ax, (Ax_t jest dodatnie) i sumując je względem i otrzymujemy

s < a < S .

Dla ustalonego podziału sumy s i S są już ustalonymi liczbami, natomiast suma <r jest zmienna — zależy od wyboru punktów £,. Jednakże, łatwo zauważyć, że przez odpowiedni wybór punktów można otrzymać wartości /(£,) dowolnie mało różniące się albo od m_t, albo odM,, a tym samym sumę a można dowolnie przybliżyć do s lub do S. Wobec tego poprzednie nierówności prowadzą do następującej, już ogólnej uwagi: przy danym podziale przedziału sumy Darboux s i S są odpowiednio kresami górnym i dolnym sum całkowych.