MATEMATYKA130

250 V. Całka oznaczona

c) Korzystając z zadania b) wykazać, że z istnienia całki J|f(x)|dx

a

b

nic wynika istnienie całki Jf(x)dx.

n

b    «

2.    Obliczyć: Jf(x)dx-t Jf(x)dx.

a    b

3.    Na podstawie definicji obliczyć: a) J xdx, b) J

o    2

4    Na podstawie interpretacji geometry cznej, obliczyć:

1    i    0    2

a)J(2-x)dx. b)J|2-xjdx, c)|xdx. d) |V4-x^:dx,

1 0 2 -2

S    J

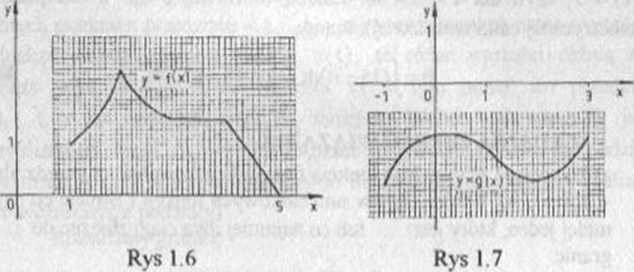
e) przybliżone wartości całek J f(x)dx i Jg(x)dx, jeśli funkcje

i    -i

podcałkowe mają wykresy podane odpowiednio na rysunkach 1.6 i 1.7.

Odpowiedzi.

I b) Wskazówka rozważyć dwn citągi sum częściowych i w jednym jako punkty pośrednie x, przyjąć liczby wymierne, w drugim zaś - liczby niewymierne.

2. 0.

ł a) 2, b) 1/4, wskazówka: przyjąć x, = VvT^x, •    S_n - consl « 1/4

•1    n)4. b) 5/2. ,c) -2, d) 2n.

2. OBLICZANIE I WŁASNOŚCI CAŁKI OZNACZONEJ.

TWIERDZENIE NEWTONA-LEIBN1ZA Poznamy tera/ bardzo prosty sposób obliczania całki oznaczonej przy założeniu, żc znamy jakąkolwiek funkcję pierwotną funkcji podcałkowej. Będzie to treścią najbliższego twierdzenia. Jest to podstawowe twierdzenie rachunku całkowego i jedno z ważniejszych w matematyce Wraz z twierdzeniem 2.4, wyraża ono związek całki oznaczonej z całką nieoznaczoną.

TWIERDZENIE 2.1 (Ncwtona-Leibniza) Jeśli f jest funkcją ciągłą na przedziale <ą.b> i O jest jej dowolną funkcją pierwotną, to

b

(2.1)    Jf(x)dx = 4>(b)-0>(a).

a

Równość la nazywa się wzorem [Ncwtona-Leibniza Prawą stronę tego wzoru zapisuje się zwykle w postaci |<D(x)£ albo <I>(x)^.

Dowód Punktami a = x₀ < x, <...< x_n_, < x_n - b podzielmy przedział <a,b> na przedziały częściowe <x, ,,x,> o długościach

Ax, Niech 8_n - max{Ax.....,Ax_n).

Łatwo widać, żc

<!>(b) <I>(a) = (<!>( x„) - <P( x_n_,)) + (<b( ,)-<I>(x_n ,))♦....+(<P(x,) <I><x,))-c

' n

+(<I>(X,) -*1K*,))

1*1

Funkcja <I> spełnia założenia twierdzenia Lagrangc’a na każdym przedziale <x, ,.x, >. zatem istnieją takie punkty x, <1 (x,__Mx,>.

G>(x,)-0(x,.,)=(x,-x,.,)<!>'(x,). i* 1.2 n.