029 3

sm²a+(~) sin a

-— = tga

4

tg a = -4 sin a

sin²ot= 1 - —

1 O

tg a = -4 sin a

Funkcje trygonometryczne

Do pierwszego i drugiego równania w miejsce

cos a podstawiamy - '.

4

Podnosimy - ¹ do kwadratu i przekształcamy

4

drugie równanie, dzieląc sin a przez - - (czyli mnożąc przez -4).

Przenosimy wiadome na prawą stronę.

Rozwiązujemy teraz pierwsze równanie, pamiętając, że początkowo ma ono dwa rozwiązania.

tg a = -4 sin a

sin a =

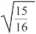
tg a - -4 sin a

Jedną z wartości sinusa odrzucamy. Jeanląsina=

Jest tak dlatego, że zgodnie z treścią zadania zajmujemy się tylko kątami II ćwiartki, a w II ćwiartce sinus jest dodatni.

sin a =

fis~ VTs_VTś

V 16 Vl6 4

Podstawiamy teraz znalezioną wartość sinusa do drugiego równania.

tg a = -4 sin a

Vl5

sin a = ——

4

tg a = -<<■— = -VT5

i

•JlJ    __

Otrzymaliśmy zatem dwie wielkości: sin a = -r- oraz tg a = -vl 5.

29