059(1)

Prędkość v i przyśpieszenie w punktu znajdziemy, obliczając pierwszą i drugą pochodną r względem /; mamy

Zatem punkt porusza się po linii prostej ze stałą prędkością, której

moduł wynosi |t>| = |^/3²+(—4)² = 5.

2) W tym przypadku torem punktu jest elipsa, określona równaniami parametrycznymi = 2cos/, z = sin/ lub też równaniem ^-+2²=1.

Elipsa ta leży na płaszczyźnie xOz.

Punkt ma prędkość v = ż = —2sin ż • i+cos/ • k i przyśpieszenie w =

—    r — —2cos/ • i—sin/ • k.

3)    Równania parametryczne toru punktu x = 2/²—3, y — —3l², z =

= 4/²—5 po wprowadzeniu nowego parametru t_x = t² przyjmą postać x= = 2ti—3,    y == —3t_u z = -lt_l—5 lub, po wyrugowaniu parametru,

-iii =    skąd wynika, że torem punktu jest linia prosta.

Punkt porusza się z prędkością v = r = 4/j—6//+8/A; przyśpieszenie ruchu w = 'r= 4/—6/+8A jest stale (nie zależy od czasu /).

Mamy więc tu do czynienia z ruchem prostoliniowym jednostajnie przyśpieszonym.

4)    Torem punktu jest tu linia śrubowa ,v = asinw/, y — acoscof, z = bt nawinięta na walec kołowy. Prędkość punktu v = r = aco coscof • /—

—    aa> sino>/ -j+bk, a przyśpieszenie w = ? = — ao>²sinw/ • i—aa>²coscot ■/. Ruch punktu jest jednostajny, ponieważ moduł prędkości |v| =

= t a²(o^Zjrb² ma wartość stalą.

298. Znając równanie ruchu punktu r = cos³/ • t+sin³/ • j wykreślić tor punktu oraz wektory prędkości i przyśpieszenia w chwili t = nf6 i t — yr/4.

Torem punktu, czyli hodografem wektora r jest asteroida x = cos³/, y = sin³/.

W dowolnej chwili / punkt ma prędkość v = r = —3cos²/sin/• i+ -f- 3 sin² / cos / • j i przyśpieszenie w> = r = 3 cos / (3 sin² / — 1) i + +3 sin /(3cos²/—1)/\

Dla / = ji/6, otrzymujemy

9

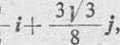
H> =

3]/3

8

^v = -ttf (/—0.

2]/2 2 J 2

Tor punktu oraz wektory prędkości z przyśpieszenia punktu w chwili t = rr/6 i t — nj4 zostały pokazane na rys. 48.

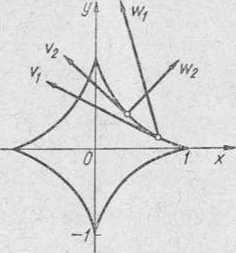
Rys. 48

W zad. 299—301 mając dane równania wektorowe ruchu punktu wykreślić tor punktu oraz wektory prędkości i przyśpieszenia w chwili t = 0 i t = 1.

299.    r = acost • i+asin/ •/

300.    r = 3tj+(4t-t²)k

301.    r = 3(f—sin/)/+3(l— cosf)y