064(1)

(5)

Błąd przybliżenia wynosi

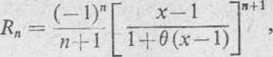
, 0 < 0 < 1

Podstawiając t = .v—1, otrzymamy

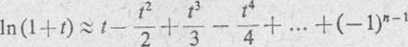
n

iH

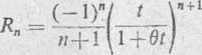
W tym przypadku tylko dla —1 < t ^ 1 reszta R„ -> 0, gdy n rośnie. Innymi słowy, błąd wynikający z obliczania logarytmów wg wzoru (5) można sprowadzić do dowólnie małej wartości tylko dla tych wartości t, które znajdują się we wskazanym półotwartym przedziale.

Dla ;i= 1, 2, 3 otrzymamy następujące przybliżone wzory

ln(l+0 s: t

t²

ln (1 + 0 ~ t—2"

t² f

ln(1 + 0 ~    2⁺ T

W sposób analogiczny jak w zad. 302 i 303 posługując s:ę wzorem Taylora możemy za pomocą najprostszych funkcji algebraicznych, tj. wielomianów, przedstawić w sposób przybliżony wiele innych funkcji przestępnych i złożonych funkcji algebraicznych, z dowolną żądaną dokładnością, co ma duże znaczenie teoretyczne i praktyczne.

304. Obliczyć z dokładnością do 10-⁶ przybliżone wartości: 1) cos5°, 2) sin 49°, 3)] 83, 4)j/l2T.

Rozwiązanie: 1) Skorzystamy z przybliżonego wzoru na cos.r, otrzymanego przy rozwiązywaniu zad. 302. Wyrażając we wzorze tym kąt 5 w radianach (w mierze łukowej)

otrzymujemy

130

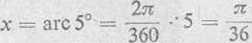
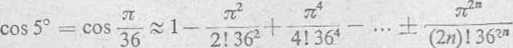
Aby określić, ile początkowych wyrazów tego wzoru należy uwzględnić w rachunku w celu uzyskania żądanej dokładności, oszacujemy wielkości kolejnych reszt J?₂,_n+1

^R] I ^ 2! ⁼ 2!3+ < °’⁰⁰⁴

= 4^5-4 < °>⁰⁰⁰ 003

[*s| < ^- = -^<0,000 000 03

Jak widać, R₅[ < 10"⁶. Dlatego też, aby osiągnąć wymaganą dokładność, wystarczy uwzględnić trzy początkowe wyrazy wzoru, poprzedzające R_s

2    4

cos 5° a 1 - ₂ ⁷¹ ^    J « 1 - 0,003 807 7+0,000 002 4 * 0,996 195

Dla zapewnienia wymaganej dokładności, wartość liczby rr oraz wszystkie pośrednie wyniki pisaliśmy z nadmiarem jednego miejsca dziesiętnego, czyli z dokładnością do 10~⁷ (rr s 3,141 591 7).

2) Aby obliczyć sin49°, piszemy wzór Taylora dla funkcji sinx

sin x

, x—a . I tc \    (x—a)² . I , _ Ti

= sma+-y|—sin a+—J++-_2! <sin|a+2 • --

+ ... +    — sin (fl+7

"■^)+Xn

+*t}

_D _ (x—o)^n+ł . (n+1)! ^Sin

R„

x—a

!n + l

(«+!)!

, gdyż | sin a| < I

Z wzoru tego można obliczać wartości sin.v dla dowolnych wartości x i a z dowolną żądaną dokładnością, ponieważ w miarę zwiększania ilości wyrazów w tym wzorze błąd R„ maleje nieograniczenie, dążąc do zera. Przy tym, im mniejsza będzie wartość różnicy \x—a\, tym mniej trzeba brać początkowych wyrazów wzoru, aby osiągnąć dowolną, z góry daną dokładność obliczeń.

9*

131