074(1)

350. y = e~^x+e'^x 352. y = xre~^x 354. y — sin jc+cos x 351. y = 3.v-)-tg a:

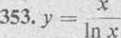
355*. y — ’ X³ ■ 3.r²

§ 5. Największa i najmniejsza wartość funkcji

Przez największą wartość ftmkcji rozumiemy największą ze wszystkich jej wartości, a przez najmniejszą — najmniejszą ze wszystkich jej wartości.

Funkcja może mieć tylko jedną wartość największą i tylko jedną wartość najmniejszą lub może nie mieć ich w ogóle. Na przykład w całym swym obszarze określoności funkcja sin* ma wartość największą równą jedności i wartość najmniejszą równą minus jedności; funkcje tg a* i .r* nie mają ani największej, ani najmniejszej wartości; funkcja —x² ma wartość największą, równą zero, ale nie ma wartości najmniejszej; funkcja 1+]. x\ ma wartość najmniejszą, równą jedności, nie ma jednak wartości największej (rys. 58).

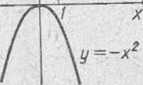
Rys. 58

Przy poszukiwaniu największej i najmniejszej wartości funkcji ciągłych opieramy się na następujących własnościach tych funkcji:

1)    Jeśli w pewnym (skończonym lub nieskończonym) przedziale funkcja f(x) jest ciągła i ma tylko jedno ekstremum, i jeśli jest to maksimum (mini-, mum), to jest ono największą (najmniejszą) wartością funkcji w tym przedziale.

2)    Funkcja f(x) ciągła u> pewnym przedziale [a,b], musi przybierać w tym przedziale największą i najmiejszą wartość. Wartości te funkcja osiąga bądź w punktach ekstremum, leżących wewnątrz odcinka, bądź też na krańcach przedziału.

Wynika stąd praktyczny sposób szukania największej lub najmniejszej wartości funkcji f(x) w przedziale [a, b], gdzie funkcja jest ciągła:

I.    Znajdujemy punkty krytyczne, leżące wewnątrz przedziału [a, 6] i obliczamy, jakie wartości przybiera funkcja w tych punktach (nie badając, czy są to ekstrema i jakiego są one typu).

II.    Obliczamy wartości funkcji na końcąch przedziału, czyli f(a) i f(b). Tli. Porównujemy otrzymane wartości funkcji; największa z nich jest

największą wartością funkcji w całym rozważanym przedziale, a najmniejsza — najmniejszą wartością funkcji w tymże przedziale.

356. Znaleźć największą i najmniejszą wartość poniższych funkcji:

1)    u = ;c³—3;r—9.v-f35 w przedziale [—4, 4]

2)    p — a²lna: w przedziale [1, e]

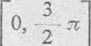
3) r — 2sin.v j-sin2x w przedziale

4) y = aretgar

Rozwiązanie. Postępujemy w myśl podanej wyżej reguły.

1)    T. Znajdujemy punkty krytyczne funkcji u leżące wewnątrz przedziału [—4, 4] i obliczamy jej wartości w tych punktach. Mamy u' = 3x²—6x—9 oraz «' = 0w punktach x = — 1 i x'= 3. Punkty te leżą wewnątrz przedziału [—4, 4] i są punktami^krytycznymi danej funkcji, jest ona bowiem określona i ciągła na całej osi liczbowej. Tnnych punktów krytycznych nie ma, bo pochodna u' istnieje wszędzie. Funkcja przybiera w punktach krytycznych wartości: k(—1) = 40, h(3) = 8.

II.    Obliczamy wartości funkcji na końcach przedziału [—4, 4]; w(—4) = = -41, «(4) = 15.

III,    Porównując obliczone wartości funkcji w punktach krytycznych i na końcach przedziału, wnioskujemy, że największa -wartość funkcji w przedziale [—4,4] wynosi 40 i znajduje się w wewnętrznym punkcie krytycznym x = — 1, a najmniejsza jej wartość wynosi —41 i znrjduje się na lewym krańcu przedziału x = —4 (rys. 59).

2)    I. Szukamy punktów krytycznych: p' = *(1+2lna:); p — 0, gdy *1 = 0 i gdy x₂ = e~^1/2. Punkt x_t leży poza obszarem określoności badanej funkcji, tj. poza przedziałem 0 < x < +co, a punkt x₂ leży poza rozważanym przedziałem [1, e]. Pochodna p istnieje w całym przedziale określoności funkcji, zatem wewnątrz rozpatrywanego przedziału nie ma w ogóle punktów krytycznych.

II.    Obliczamy wartości funkcji p na końcach przedziału: p(l) = 0, p{e) = e¹.

III.    Ponieważ wewnątrz przedziału [l,e] nie ma punktów krytycznych, więc funkcja zmienia się w nim monotonicznie, a największą i najmniejszą

151