084(1)

3'J3. Zbadać funkcje i sporządzić ich wykresy:

3'J3. Zbadać funkcje i sporządzić ich wykresy:

3) y = | (x-fl)²-V (^x~ l)² » 5) y - X¹ | e

*2 )y--—jr-4) y — sin⁴* 4- cos⁴x 96) y — A' 2arc ctg x

l)*y = |<?^x-l,|

Rozwiązanie. Kierując się podanym ogólnym schematem, znajdujemy kolejno:

1) I. Dana funkcja, jak wszystkie wielomiany, jest określona na całej osi liczbowej.

TT. Funkcja nie ma punktów nieciągłości i jak każda funkcja elementarna jest ciągła wszędzie tam, gdzie jest określona.

III.    Funkcja nie jest parzysta ani nieparzysta, ani też okresowa.

IV.    Dla x — 0 z danego równania znajdujemy y — 0. Z kolei dla y — 0, otrzymamy x — 0 lub x — 4, co oznacza, że wykres funkcji przecina osie współrzędnych w punktach (0, 0) i (4, 0).

Przedziały, w których funkcja zachowuje stały znak, wyznaczamy z warunku, że ich krańcami mogą być wyłącznie albo punkty przecięcia się try-kresit funkcji z osią Ox, albo punkty nieciągłości, albo też wreszcie brzegi obszaru określoności funkcji.

Dla badanej funkcji takimi punktami są x = 0 i .v — 4. Określając znak funkcji dla dowolnej wartości ,v z przedziału (—oo, 0), np. dla x= 1, znajdujemy, że y(— 1) < 0, a tym samym stw ierdzamy, że w całym tym przedziale funkcja przybiera wartości ujemne. Analogicznie stwierdzamy, że w całym przedziale (0, 4) funkcja ma wartości dodatnie, bo y(l) > 0, oraz że jej wartości w przedziale (4, +co) są ujemne, mamy bowiem

j(10) < 0.

V.    a) Funkcja jest wszędzie ciągła, wobec czego jej wykres nie ma asyrn-ptot pionowych.

b) Znajdujemy    ,

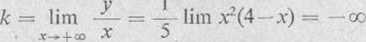
Nie istnieje też współczynnik kątowy k asymptoty, kiedy .v -» oo. Zatem wykres funkcji nie ma asymptot nie pionowych.

/ = *-(12x²-4.v³) = ~x^l(3~x)

i równa się zeru w punktach x — 0 i x — 3. Są to punkty krytyczne; wszystkie niezbędne do tego warunki są w nich spełnione. Innych punktów krytycznych nie ma, gdyż pochodna y^K wszędzie istnieje.

Badamy punkty krytyczne wyznaczając znak y' w ich otoczeniu:

X	-i	0	1	3	10
/	4-	0	+	0	-
y	roś.	nie ma - ekstr.	roś.	max	mai.

Punkt x = 3 jest więc punktem maksimum funkcji: y_max — j(3) =    - =

= 5,4.

Przedziały monotoniczności funkcji, w których funkcja wzrasta bądź maleje, znajdujemy na mocy warunku, że granicami tych przedziałów mogą być wyłącznie punkty ekstremum, punkty nieciągłości i punkty ograniczające obszar stanowiący dziedzinę funkcji.

Funkcja badana jest wszędzie ciągła i ma tylko jeden punkt maksimum x = 3. Wobec tego w przedziale ( -oo, 3) funkcja rośnie, a w przedziale (3, +co) maleje.

12

VII. Druga pochodna y" — - — x(2—x) istnieje wszędzie i jest równa

zeru dla v = 0 i ,\- = 2. Te wartości a- mogą więc być odciętymi punktów przegięcia. Badamy je określając znak/' w'ich otoczeniu:

*	-i	0	J	2	10
	-	0	4.	0	-
y 1	wyp.	pkt przeg.	wid.	pki przeg.	wyp-

Wykres funkcji ma zatem dwa punkty przegięcia (0; 0) i (2; 3,2) (rzędne tych punktów zostały obliczone przez podstawienie odciętych do wyrażenia na funkcję).

171