060(1)

ROZDZIAŁ III

BADANIE FUNKCYJ ORAZ SPORZĄDZANIE ICH WYKRESÓW § 1. Twierdzenie (wzór) Taylora

Liczne zastosowania rachunku różniczkowego w naukach przyrodniczych i w technice są oparte na twierdzeniach Rolle’a, Lagrangc’a, Cauchy'eeo i Taylora. W każdym z tych twierdzeń mówi się o istnieniu pewnej średniej wartości argumentu x = c, w związku z czym nazywamy je twierdzeniami o wartości średniej.

TWIERDZENIE TAYLORA. Funkcja f(x) róźnićzkowalna n fl razy w pewnym przedziale zawierającym punkt a daje się przedstawić jako suma wielomianu stopnia n oraz reszty R„

m -m£ff <*-«)₊qs    O -»>>+

(T)

przy czym c jest tu pewną wartością średnią zawartą między a i x c = aĄ-0(x — a),    0 < 0 < 1

Jest to najogólniejsza postać twierdzenia o wartości średniej, z którego wynikają wszystkie pozostałe.

Wzór Taylora (T) pozwala przedstawiać w sposób przybliżony (aproksy-mować) dowolną funkcję/(.x) za pomocą wielomianu

/(*)-/(*)-

f'(a)

1!

f"(d)

(*-a)+ ^J- (x-a)²+ ... +4%-^ (*)

ni

(zwanego wielomianem Taylora). Jednocześnie wzór ten pozwala oszacować powstały przy tym błąd. W wielu przypadkach błąd ten można uczynić dowolnie małym. Z tego powodu wzór Taylora jest jednym z najważniej-

szych wzorów analizy matematycznej; jest on szeroko stosowany i jako subtelne narzędzie badań teoretycznych, i jako wzór rachunkowy przy rozwiązywaniu wielu zagadnień praktycznych.

Szczególną, prostszą postać wzoru Taylora, gdy a = 0, nazywamy wzorem Maclaurina

(Mj

Wzór ten tiaje rozkład funkcji wg potęg samej tylko zmiennej niezależnej. Jednakże dla wielu funkcji nie można stosować prostszej postaci wzoru Taylora, ponieważ wiele funkcyj bądź też ich pochodnych nie ma określonej

jnp. In*, j

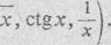
w artości dla * = 0

302. Funkcje: 1) e^x, 2) sinjc, 3) cos* przedstawić w postaci wielomianów stopnia n względem *, oszacować błąd oraz ustalić, dla jakich wartości * błąd ten można uczynić dowolnie małym.

Rozwiązanie. Aby otrzymać przybliżone przedstawienie danej funkcji /(*) w postaci wielomianu względem zmiennej niezależnej *, należy napisać dla tej funkcji wielomian Maclaurina (tj. wielomian (*) dla a = 0). Następnie, aby oszacować błąd powstały na skutek zastąpienia funkcji wielomianem Maclaurina, należy znaleźć resztę R_n wzoru Maclaurina wg ogólnego wzoru na resztę, zastosowanego do danej funkcji. Na koniec, aby wyznaczyć te wartości *, dla których błąd można uczynić dowolnie małym, trzeba zbadać, jak zachowuje się reszta, gdy n -> + oo dla różnych wartości x_r Błąd można uczynić dowolnie małym tylko dla tych wartości ,v, dla których lim J'_n = 0.

1) Obliczywszy wartości danej funkcji i jej pochodnych dla * = 0

/•(*) -    /'(*) =/"(*) =/"'(*) = - -/“'W = e^x

/(O) =/'(0) =/"(0) = ... =/⁽‘^,(0) = 1

posługując się wielomianem Maclaurina (*), otrzymamy poszukiwane przybliżone wyrażenie danej funkcji przestępnej w postaci wielomianu stopnia n

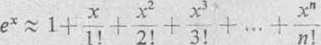
(1)

123