090 091 2

90 Programowanie liniowe

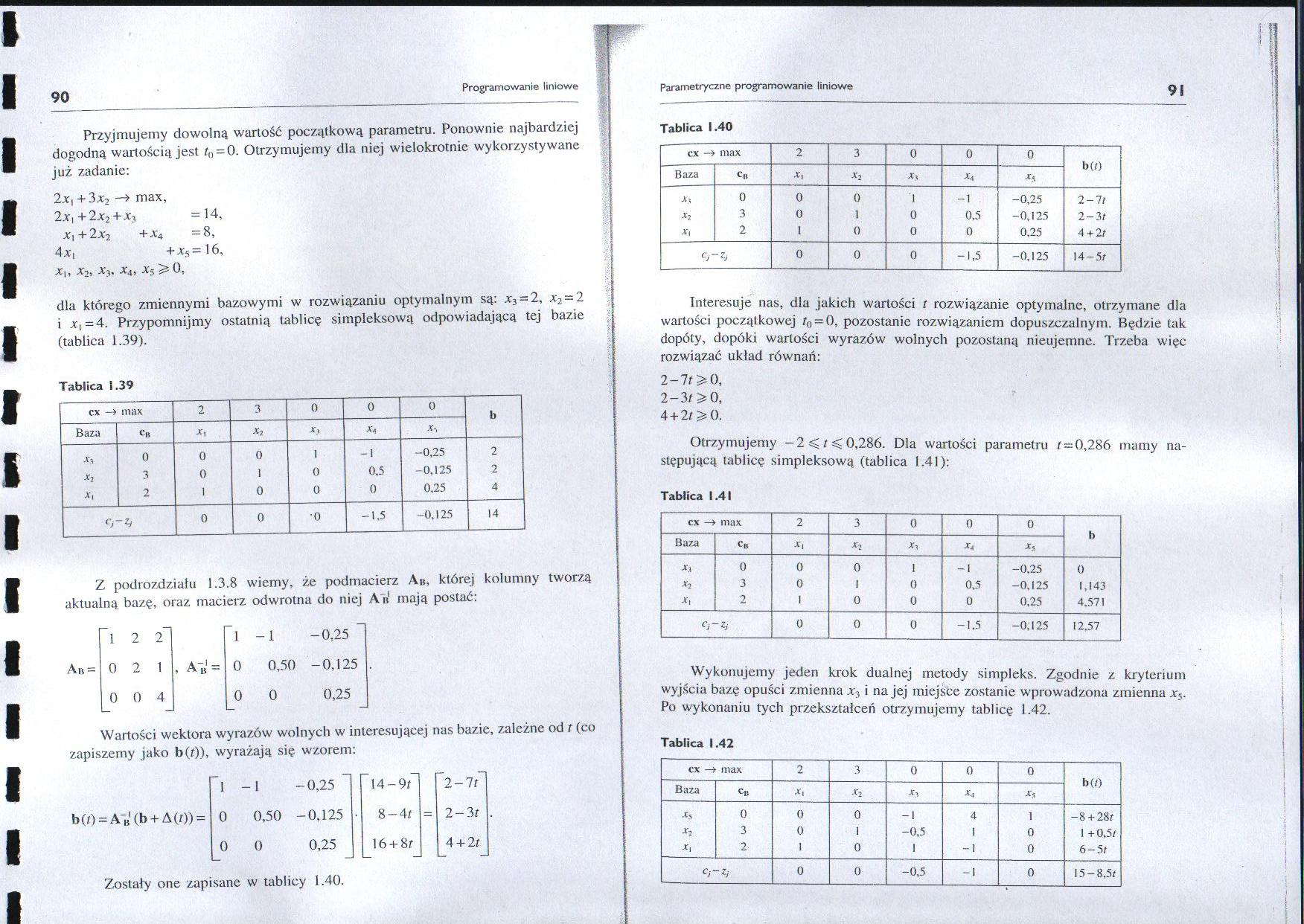
Przyjmujemy dowolną wartość początkową parametru. Ponownie najbardziej dogodną wartością jest /„ = 0. Otrzymujemy dla niej wielokrotnie wykorzystywane już zadanie:

2x, + 3*₂ —» max,

2x i + 2*₂ +*₃    ⁼ 14,

*i+2*₂    +-*₄    =8,

4*i    +Jt₅=16,

*,, *2. •*+ *4, -*5 > o,

dla którego zmiennymi bazowymi w rozwiązaniu optymalnym są: *₃ = 2, *₂ = 2 i *|=4. Przypomnijmy ostatnią tablicę simpleksową odpowiadającą tej bazie (tablica 1.39).

Tablica 1.39

cx -»	max	2	3	0	0	0	b
Baza	C„	*1	*2	Xy	^X4	X•,
Xy	0	0	0	1	-1	-0,25	2
*!	3	0	1	0	0,5	-0,125	2
*1	2	1	0	0	0	0,25	4
^cr	"9	0	0	•o	-1.5	-0.125	14

Z podrozdziału 1.3.8 wiemy, że podmacierz Ab, której kolumny tworzą aktualną bazę, oraz macierz odwrotna do niej Ab mają postać:

	^_1	2 2		~1	-1	-0,25 ~
An =	0	2 1	, Aj,^1 =	0	0,50	-0.125
	0	0 4		0	0	0,25

Wartości wektora wyrazów wolnych w interesującej nas bazie, zależne od / (co zapiszemy jako b(r)), wyrażają się wzorem:

	~\ -1	-0,25 ~		^_ 14 — 9/^_		"2-7f“
b (/) = Aj,^1 (b + A (/)) =	0 0,50	-0,125		8 — 4/	=	2-3/
	0 0	0,25		16 +8r		4 + 2/

Zostały one zapisane w tablicy 1.40.

Tablica 1.40

cx —»	max	2	3	0	0	0
Baza	C»	x,	*2	X*
	0	0	0	i	-1	-0,25	2-Tl
*2	3	0	1	0	0.5	-0,125	2-3/
	2	1	0	0	0	0,25	4 + 2/
^cr	-Z,	0	0	0	-1,5	-0,125	14-5/

Interesuje nas, dla jakich wartości / rozwiązanie optymalne, otrzymane dla wartości początkowej /₀ = 0, pozostanie rozwiązaniem dopuszczalnym. Będzie tak dopóty, dopóki wartości wyrazów wolnych pozostaną nieujemne. Trzeba więc rozwiązać układ równań:

2—7f > 0,

2-3/>0,

4 + 2/>0.

Otrzymujemy — 2</<0,286. Dla wartości parametru / = 0,286 mamy następującą tablicę simpleksową (tablica 1.41):

Tablica 1.41

cx —	max	2	3	0	0	0
Baza	C«	^x\	X2		Xą	x,
X\	0	0	0	i	-i	-0,25	0
*2	3	0	i	0	0,5	-0.125	1,143
	2	1	0	0	0	0.25	4.571
Cj-	-z,	0	0	0	— 1,5	-0.125	12.57

Wykonujemy jeden krok dualnej metody simpleks. Zgodnie z kryterium wyjścia bazę opuści zmienna i na jej miejsce zostanie wprowadzona zmienna jc₅. Po wykonaniu tych przekształceń otrzymujemy tablicę 1.42.

Tablica 1.42

cx —	max	2	3	0	0	0	b(/)
Baza	^CB	X,	*2	xy	JCj	*5
Xj	0	0	0	-i	4	i	-8 + 28/
x2	3	0	1	-0,5	1	0	1 +0,5/
X,	2	1	0	1	-1	0	6-5/
o-	-Z/	0	0	-0,5	-1	0	15-8.5/