092(1)

nieograniczonych gałęzi, z których każda przecina prostą y = *. Równanie to ma więc nieskończenie wiele pierwiastków rzeczywistych. Najmniejszy dodatni pierwiastek x, tego równania jest zawarty w przedziale [0,8; 0,9].

408. Obliczyć z dokładnością do 0,0001 największy spośród pierwiastków równania*⁵—*—0,2 = 0.

Rozwiązanie. Najpierw oddzielamy szukany pierwiastek metodą graficzną. Pisząc równanie w postaci *⁵ = x+0,2 i wykreślając krzywe y = x⁵ iy = *+0,2 w jednym układzie osi współrzędnych (rys. 85) stwier

dzamy, że poszukiwany największy pierwiastek zawiera się w przedziale

[i; U]-

Następnie obliczamy przybliżoną wartość pierwiastka z przyjętą dokładnością posługując się metodą siecznych i stycznych, czyli stosując wzory (*) do zawężenia przedziału zawierającego pierwiastek.

Zanim jednak zaczniemy wzory te stosować, trzeba sprawdzić, czy funkcja/(*) == *⁵—*—0,2 i znaleziony przedział czynią zadość niezbędnym warunkom, to znaczy, czy:

a)    wartości funkcji /(*) na końcach przedziału mają przeciwne znaki,

b)    pierwsza i druga pochodna funkcji zachowują w tym przedziale swój znak.

Mamy:

a)    /(l) = -0,2 < 0,    /(1,1) = 0,31051 >0

oraz

b)    /'(*) = 5*⁴— 1 > 0,    /"(*) = 20*3 > o

dla wszystkich wartości * z przedziału [1; 1,1].

Ponieważ/(*) i /"(*) mają jednakowe znaki, gdy * = 1,1, więc oznaczając końce przedziału przez a= 1, b — l,\ — fi i stosując wzory (*), otrzymamy

0,1 • 0,2

Do otrzymanych nowych granic u, i b_{ węższego przedziału zawierającego szukany pierwiastek stosujemy ponownie wzory (*); mamy

0,059 5

*1 =

1,1

/(U)

/'(1,1)

0,310 51 0,320 5

1,051

= a,-    = 1.039+°>⁰¹;.^² = 1,044 69

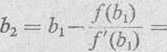
1,051 —

0,031 3 5,100 5

1,044 87

Długość odcinka [a₂, b₂\ nie przekracza dwukrotnej wartości dopuszczalnego błędu, ponieważ \a₁—b₂\ = 0,000 18 < 2 • 0,000 1. Zatem szukana przybliżona wartość największego pierwiastka danego równania z dokład-

^2“ł“^2

nością do 0,000 1 wynosi x₀ ~ —₂—= 1,044 8.

409. Obliczyć z dokładnością do 0,000 001 pierwiastek rzeczywisty równania 2—x—lgx — 0.

Rozwiązanie. Aby oddzielić szukany pierwiastek, zapisujemy równanie w postaci !gjvr = 2—cc i kreślimy krzywe y = lg.r i y = 2—x (rys. 86). Z wykresu odczytujemy, że szukany pierwiastek zawiera się wewnątrz przedziału [1,6; 1,8].

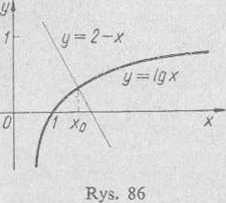
Dla sprawdzenia warunków, które muszą być spełnione przy korzystaniu z metody siecznych i stycznych, obliczamy wartości funkcji f(x) = 2—x— — lgx na końcach wyznaczonego przedziału oraz znajdujemy pochodne

/'(*) i /"(*)

/(1,6) = 2-1,6 - 0,2041 = 0,1959 > 0 /(l ,8) = 2-1,8-0,2553 = -0,0553 <0

187