093 2

Równania trygonometryczne

I znowu, pierwsze rozwiązanie zawiera drugie x — — + 2kn.

Stąd rozwiązaniem układu jest

x = ^ = 2kn, k e C.

2

Odpowiedź

x = 2kn lub x = j = 2kn, k e C.

II sposób

Rozwiążmy równanie sin x + cos x = 1 inną metodą.

cos x = 1 • cos x

i

, 7C ^1=t§7

Wstawiamy do równania wyjściowego za 1 stojące

pr2y cos x wartości tg Następnie zamieńmy funkcję

tg u =

sin o. cos u'

sin x + tg - cos x^:

1 /•cos -4

k . k    , n

sin x ■ cos - + sin - • cos x = 1 • cos -4    4    4

Po lewej stronie równania korzystamy ze wzoru: sin (« + |S) = sin a • cos (i + sin (i • cos a.

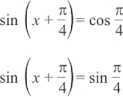
TC

4

Znalezioną wartość kąta wstawiamy do wzorów rozwiązań równań: sin x = a.

TC    K    TC    ,

= - + 2hc lubx + - = 7t-- + 2kie 4    4    4

93

X