099 2

Nierówności trygonometryczne

ZADANIE 3

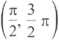
Rozwiąż nierówność: tg x < x3, x e

Rozwiązanie:

Rysujemy wykres funkcji tangens w przedziale ~ n

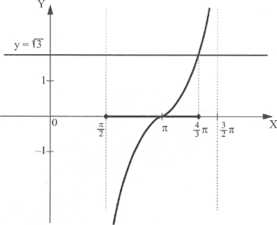
Rysujemy wykres i rozwiązujemy pomocnicze równanie

tgx=V3 x₀ = 5

x = x₀ + bt - ^ + Im, keC

x =    + Im, k e C

dla k = 1 mamy:

x = j+1-rt = | + jt = j>t

ten punkt należy do przedziału ^ rt

Pytamy, kiedy wykres funkcji tangens leży pod prostą_y = V3? Po uwzględnieniu rozwiązania równania pomocniczego mamy:

Odpowiedź

(n 4

1 - - 71

\2 3

99