mat6

7. FUNKCJE TRYGONOMETRYCZNE

9.    Rozwiązać w zbiorze liczb ujemnych równanie |sin⁴x—cos⁴x| = y.

10.    Dla jakich wartości xe<0;7t> jest spełniona nierówność cos2x + cosx—1 ^

cos2x

11.    Znaleźć największy ujemny pierwiastek równania sinx + cosx = y/2.

12.    Rozwiązać równania:

a) cosxcos6x + l =0,    b) sin²⁹3x — cos¹⁷10x = 2.

13.    Dla jakich x prawdziwa jest równość

1 + tgx + tg²x + ... = -?

l-tgx

14.    Rozwiązać równanie

1 — sinx + ... +( — l)"sin"x+ ... _ 1—cos2x l + sinx+ ... + sin"x + ...    l + cos2x'

15.    Znaleźć najmniejszy dodatni pierwiastek równania (sin4x + sin2x)² + sin²x = 1.

^ jest spełniona nierówność

—-K

tg2x—ctg2x >

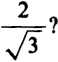
17. Dla jakich xe

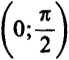
<0?

są spełnione nierówności

l _c ³tg^JC-ctg^x

18. Udowodnić, że dla każdego rzeczywistego x

1    .    .    7

— < 2 + sinx—cosx < —.

2    2

19. Znaleźć najmniejszą liczbę x spełniającą warunki

= 1 i x > Sn i ctgx > 0.

2x

sin-

20. Rozwiązać dla xe<0;2jr> nierówność cos²x + cos³x + cos⁴x + ... < l+cosx.

21. Rozwiązać układy równań:

1

{sinxcosy = —

_r c

4cOSXCOSy = ,^3 ,

x+y =

76

ir» v — —-

smx+siny =

k i) j

l tgx + tgy = 1,

2 ’

f tgx —tgy = 2 }ctgx —ctgy = 2.

22. Dla jakich wartości parametru m należących do przedziału

d)

^0; —j równanie x²sinm + x + cosm = 0 ma dwa różne pierwiastki rzeczywiste?

23. Dane jest równanie (2cosy—l)x² —2x + cosy = 0, gdzie y jest rametrem. Dla jakich wartości y e <0; 7r> równanie ma dwa różne ierwiastki rzeczywiste?

24. Dla jakich wartości parametru m równanie sin⁴x + cos⁴x = m a rozwiązania?

25.    Rozwiązać w przedziale (0; 7t) równanie

»*' ₂Wx+i ₊ i6.2⁴»»^J*-3 = 20.

26.    Rozwiązać równanie

^.^jl-cos²x_y.2sin²x __ g

f 27. Dla jakich wartości parametru w równanie l+sin²mx = cosx a dokładnie jedno rozwiązanie?    ■

95