10(7)

tor a / rysunku 3.8;t jest dany (t/.n. całkowicie wyznaczony) przez wielkością i 0. Można go również określić, podając składowe r/_v i u_y. Obie pary wielkości /.uwierają ly samą informację. Są one ze sobą powiązane zależnościami:

a =

oraz

a_v

— —.

“x

(3.6)

W bardziej ogólnym przypadku trójwymiarowym wektor jest wyznaczony przez jego długość i dwa kąty (np. </, 0 i (f>) lub jego trzy składowe (</,. a_y i a.y

^SPRAWDZIAN 2: Nil którym / |x>ni/szych rysunków poprawnie wyznaczono wektor <? nu podstaw ie jego składowych .\ i r?

i

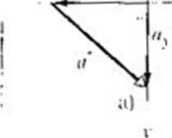
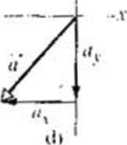
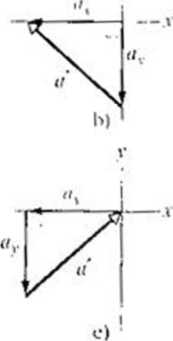
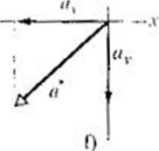
2(K)

c

()•

■ U

IDO

odległość |km]

Przykład 3.2

Muły samolot wystartował /. tomiska i wkrótce przestał być widoczny, gdyż niebo l»\!o zachmurzono. Dosli/.o/ono go dopiero .w odległości 21.5 km od lotniska, w kierunku północno-wschodnim. tworzącym kat 22 / kierunkiem północnym. Jak daleko na północy i jak daleko na wschodzie znajdował się wówczas samolot?

ROZWIĄZANIE:

O—r Mamy dane: długość wektora <2! tf* km.i i kat jaki tworzy on / pewnym kierunkiem (22 na wschód od kierunku północnego). a musimy wy/.nuc/.yć sklądowe tego wektora. Narysujmy układ współrzędnych .w tak. że kierunek dodatni osi .v jest kierunkiem ku wschodowi, a osi v — ku jtółnocy (rys. 3.10). Dla wygody wyhicr/.my początek tego ukhulu w miejscu, w którym znajduje się lotnisko. Tak więc wektor przemieszczenia samolotu z/ ma początek w początku układu, a koniec w' punkcie, w którym dostrzeżono samolot.

Aby obliczyć składowe wektora <1. korzystamy / równania (3.5), do którego podstawiamy H = 68 (-- 90 — 22 ). co daje .. >•/» </ » /

z HIO

Rys. 3.10 Przykład 3.2. Samolot wystartował / tomiska umieszczonego w początku układu współrzędnych. a po pewnym czasie został dostrzeżony w punkcie /¹

di = <1 cos0 (215 km)(cos6R ) = 81 km.    (odpowiedź)

d_y = dsinO = (215 km)(sin68 )    199 km.    (odpowiedź)

Dany samolot oddalił się załom od lotniska o 81 kin na wschód i o 199 km na północ.

42    3. Wektory

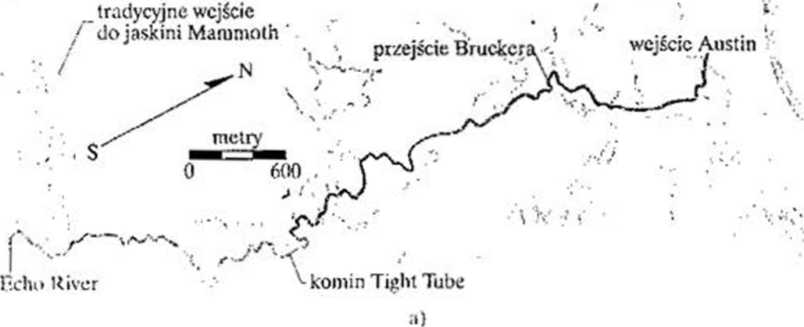
^spół groto! a/.ów. któr/y w 1972 roku dokonali przejścia / jaskini Flint Ridge. wchodząc do niej wejściem Austin, do licho £jver w jaskini Maimnoih (rys. VI la), i dowiedli w len sposób, że jaskinie te s;j połączone. przemieścił się łącznie 2.6 km na 2achód. 3.^ km na południc i 25 m do góry. Wy znać*/ wektor przemieszczenia tego zespołu, od punktu wyjściowego do punktu końcowego wędrówki.

ROZWIĄZANIE:

O—ł Dane są składowe wektora trójwymiarowego. a należy wyznaczyć jego długość i dwa kąty. określające jego kierunek. Najpierw narysujmy te składowe w uklail/.ic współrzędnych, jak na rvstmku 3.1 Ib. Składowe poziome (2.6 km na zachód i 3.9 km na południe) są pr/ypiosiokątnymi poziomego trójkąta pioMokąl-neao. Przemieszczenie w poziomie jest przeeiwprostokąiną lego trójkąta, a jej długość </_h obliczamy z tw ierdzenia Pitagorasa:

d, -    (2.6 km i' •• (3.9 km)’ = 5.69 kin

Z teeo samego trój kąta poziomego na rysunku 3.1 Ib wniosku jemy. że przemic^zc/enic poziome zespołu jest skierowane na południe orf kierunku zachodniego, pod kątem *K, danym piz.ez:

_ (3.9 kmt ^{lr 11}    (2.6 kun'

(ł„ = arclg - ' —- = 56 .    (odpowiedź)

(2.6 km)

Jest io jeden z dwóch kątów, które wyznaczają kierunek całkowitego przemieszczenia zespołu.

Aby uwzględnić przemieszczenie w pionie (25 ni = 0,025 km), narysowaliśmy (na rysunku 3.1 le) widok z boku. w kierunku północno-zachodnim. Na tym rysunku znów mamy trójkąt prostokątny, którego przy prostokątny mi są tym razem przemieszczenie w pionie i przemieszczenie w poziomie Ą. Całkowite przemieszczenie zespołu jest przeeiwprostokąiną tego trójkąta, której długość wynosi:

</ = _N (4.69 km)- t- có.025 km)*' *= 4.69 km =: 1.7 km

(odpowiedź)

lY/cmiesze/onto to jest skierowane od poziomu w górę |XHl kątem: 0.075 km

o. r. arcie • ••    • -"0. ' .    (odpowiedzi

' 4.69 km

lak więc wektor przemieszczenia zespołu miał długość 4.7 kio i był skierowany w poziomic pod kątem 56 na jioludmc od kierunku /uchodtiicgo. a w pionie — pod kątom 0.3 ku górze l.ączne przemieszczenie w pionie lwio bardzo nudo w j>oiówmj mu z przemieszczeniem u poziomic. Grotołazi nie mieli jednak z tego wielkiego pożytku, gdyż w rzeczywistości musieli nieźli c/.oną liczbę razy wspinać się i schodzić w dół. w trakcie we drów ki przez jaskinię. Przebyta przez nich droga była zupełnie inna niż wektor przemieszczenia, który jedynie łączy wzdłuż linii pi osiej punkt początkowy i ławicowy wędrówki

góra

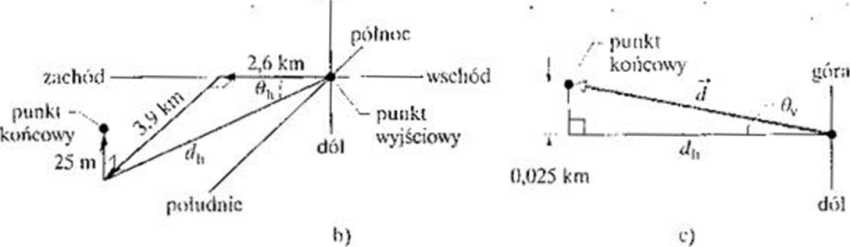
Rys. 3.11. Przykład 3.3. -i) Część układu jaskiń Mammoih -I^;łiiu z. zaznaczonym nu czerwono szlakiem zespołu speleologów od wejścia Austin do fceho Rivcr (na podstawie mapy Fundacji Badania Jaskiń), b) Składowe całkowitego przemieszczenia zespołu oraz jego przemieszczenie w poziomic </_n. c) Widok z boku, tikit-Aijący Ą, i wektor całkowitego przemieszczenia zespołu (!

3.3. Sklodovze wektorów 43