Capture175

Ważną cecha kontrastu jest 10. że jeteli 4' jest kontrastem i„ >j, przez pewna Mała równie/ jest kontrastem. Jeżeli wagi 4' sutnui,    ^{! rn}’ ⁷‘^

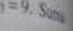
kwadratów wynikająca / wynosi:

wagi 4' również sumują m< do /eru. Niech 4*2=24' -.+£,+ ę. -.y

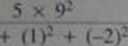
samym porównaniem.

Każdy kontrast przedstawia sobą jakąś różnicy*. Związana / kontrastem _s kwadratów jest miarą siły tej różnicy. Sumę kwadratów wykorzystuje mc do b" nia istotności tej różnicy. Badanie to przeprowadza się lak samo jak test /

18.4. Badanie kontrastów jako

przeprow adzanie porów nań planow anych

analogiczna do tej. jaka występuje w teście r. gdy r równe jest / / jednym

Z suma kwadratów, za którą odpowiedzialny jest dany kontrast, /.owe jest pewnu liczba stopnt swobody. Można się o tym łatwo przekonać, /wrac** uwagę, że kontrast przedstawia sobą różnicę między dwoma zbiorami średnich,i których jeden ma wagi dodatnie, a drugi ujemne. Jest tak niezależnie od tego, ;_t średnich rzeczywiście zaangażowanych jest w konkretne porównanie. W onxiv.i> nym wyżej 4', mamy do czynienia tylko z dwiema średnimi i badanu ram*j między nimi. W 4'- mamy do czynienia z trzema średnimi, lecz badanu rór.ą między średnią z pierwszych dwóch średnich a trzecią średnią. Z ró/mc4 dwoma wynikami zawsze związany jest jeden stopień swobody. Sytuacja jot a

pniem swobody w liczniku.

Średni kwadrat otrzymujemy tak jak w ogólnym teście I Jest to sunu U; dratów podzielona przez odpowiadającą jej liczbę stopni swobody W tym prry-padku średni kwadrat równy jest liczbie stopni swobody, ponieważ / >um;j k-i-drotów w przypadku kontrastu związany jest zawsze jeden stopień swobod)

zależnymi, jako składnik błędu można zastosować inny średni kwadrat jm/cl: ctd

Tak jak poprzednio, w celu zbadania istotności różnicy wyra/onci przez < trast. formułujemy statystykę F w postaci stosunku dwóch średnich ksudrao*. przy czym średni kwadrat, za który odpowiedzialny jest kontrast. umios/s/arr,v« liczniku, a średni kwadrat wewnątr/grupowy (czyli składnik błędu) u mianowau We w szystkich planach, z wyjątkiem planu jednoczynnikowego / grupami fa*-

_M wcwn«wzgnipow>. Na pr/ykład w pu.,,    .

(który /osijoic omówiony wn ’    -^/Vn'"^k"*vm ,

*1 Mcdu pr/yjmujcmy średni kwadra, .ntcrakcy.m .T^ ""*«*> *ko *Ui

IM.    * - c/^uam, rC ,/ 7    *

0lBiCł» Pr/y hadan.u V, . V, składnik błędu je« _(jł, ‘ '> '"^crru <^dn,m. _J4ju, ^gnłpowegc. którego c/ętf slwowu, T , p    ^,A **> Olaniu efektu

Zdefiniowana wyżej «Wystyka f w_yn,k, , _r Y.

.-iftńcy nucd/> <rcdn.mi w populacji Wykazy war^! J/ ' **'>    o braku

priori porównujemy zaobserwowany «,*, *    *'> poe<w

ryt/ni f określona w len sam sposób. _J4k pr_A , „ . ^y'^,kl f ' *»to<cia _tr, tatibody rozkładu F wynosi | dla licznika Maty* j    ' Liczba top_ni

pi /wiązane ze średnim kwadratem W planie edr * ° ^{J m,}*»*nika t>le ,ic iJe/nymi liczba stopni swobody w mianowniku '    ^/>nn,ko*y"» / grupom. _n*

„ewnątr/grupowym.    ** ^Jnosc^ '*'4/aną , efektem

Przyjmijmy, że średni kwadrat wewnątr/grupowy wv i»h 15. Wówczas F_% * 62.5/2.5 = 25. a>* /    * "“*>«■» pr/ykła

porównujemy z wartością krytyczną Fpr/y lip l_tonn- '‘    " '    *    <*

pewnie istotności u = 0.01. Wartom ta wynos, y u '^{Uoł>odv 1 nj} P«>kbd

miedzy X, a X₂ i różnica między <JP, +    /■> o    ^nicc- ^{IJ fl,/nicj}

'    ¹    M istotne

18.5. Kontrasty ortogonalne

i podział niiędzygrupowej sumy kwadratów

lak pamiętamy, w omawianym wyżej przykładzie między grupowa suma kwadratów CjDOsi 130. Pamiętamy również, że S_T| = 62.5. a S*. = b7.5. co w sumie daje 150. Aczkolwiek nic dzieje się tak dla dowolnych dwóch kontrastów, me jest to tylko przypadek. Prawidłowość taka ma charakter ogólny wówczas, gdy spełniony jot pewien warunek dotyczący wzajemnej zależności między ‘P, i 'P_:. a mianowt-

gdy i 4*. są względem siebie ortogonalne w sensie, który /ostanie wyjaśniony poniżej.

0 dwóch kontrastach mówimy, że są względem siebie ortogonalne, gdy suma iloczynów odpowiadających im wag równa jest 0. Tak więc

!>,,    = a    u*})

|

gdzie <-|, i ^ są wagami odnoszącymi się do j ej średniej odpowiednio w piórowym i drugim kontraście. Dla % i ‘P_: określonych wyżej

(iXVj) + (-1)(‘/₂) ♦ (0H-I) =0.

347