130 3

260

stopień nieokreśloności, wybrać należy te, które częściej występują _z negacją, tzn. mające większą liczbę zer w ? _min-Oba warianty są równoważne.

W sytuacji, gdy rozdział zmiennych jest dokonany, tzn. określone są zbiory X^ i X_;, należy podać postać funkcji Uj wprowadzanych na wejścia informacyjne multipleksera. W przykładzie 3.35 podano trzy metody generowania u^:

a)    na bazie tablic Karnaugha dla u^,

b)    na bazie minimalnej postaci rozważanej funkcji,

c)    na bazie zbioru ?    , .

Zaznaczono tam, że dwie ostatnie metody (równoważne sobie), w przypadku funcji niezupełnych mogą dawać bardziej złożone (choć poprawne) wyrażenia na u^ niż daje metoda pierwsza. Obecnie zilustrujemy ten problem na przykładzie.

Przykład 3.38

Rozpatrujemy funkcję opisywaną tabelą Karnaugha przedstawioną na rys. 3.63. Minimalna NPS funkcji jest następująca:

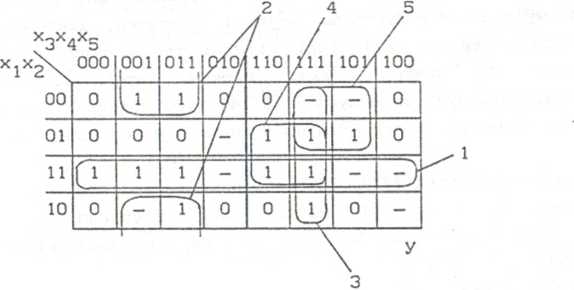
Rys. 3.63. Tabela Karnaugha funkcji z przykładu 3.38

y -f(x₁.x₂.x₃.x₄.x₅) *= xjx₂ ♦ x₂x₃x₅ * x₃x₄x₅ + x_,x₃x₄ + x_lX3x₅

(3.143)

Stosując Wariant 2 metody optymalnego rozdziału zmiennych (rys. 3.64) uzyskujemy dla multipleksera o dwóch wejściach adresowych: X_& ³ (x₂» x₃); X_i =    (Xj,x₄,Xg). Na podstawie rys. 3.64 możemy również wyznaczyć funkcje u^

x₂ x₃ x₄ Xg    (*2^x3) “ (00), (01), (10), (11)

			^X1	^X4	"^51
c o II	^u(x2x3)=(00)					=	x5,
			^X1	^X4		^X5
^U1^=	^U(x2x3)=	= (01) ^= 1	0	1		1	’ ~ ^X4^X5 ^+		^xl^x5’	(3.144)
			^X1	^X4	^X5,
^u2 ^=	^u(x2x3)=(10) " '		^1		_	\^m	^xr
			^X1	^X4	^X5
c GJ II			' 1	1	' 1				^X4
	^U(x2x3) =	=(11) ^= '	0	1	1		^X! *	^X4^X5	+ x4 + X	X Ul II
						=	^(v	Xg)(Xj + Xjj		^+ X4 =
						a	^X1^+	^x4 ^+	^x5'
Stąd
y=	MUX (x5,	^X4^X5 ^+	^X1^XE	., X	1'	^xi	^+ x4	+ Xg;	x2, x3)	(3.145

1 . 0	1 -0 0 - 1 1 1 - 1				.
		1 ___________,			----V
		— i ------ < 1 1 __________
		1 i			------
		1 — ----- 1 ______ __
		— 1 --			-----)
3 2j 1 3 2q

Rys. 3.64. Generowanie zbiorów X_a, X^ oraz określanie funkcji u. z pomocą 5*_min (przykład 3.38)

Proponujemy Czytelnikowi sprawdzenie, że zastosowanie Wariantu 1 metody °Ptymalnego rozdziału zmiennych, daje identyczne, jak wyżej, zbiory X_& ¹ X.. Określenie zaś wyrażeń opisujących Uq₁u₁,u₂,u₃ na bazie ^minimalnej postaci (3.143) rozważanej funkcji daje identyczny wynik jak