169(1)

Równania linii ograniczających obszar całkowania również należy wyrazić we współrzędnych biegunowych (za pomocą podanych wzorów na przejście od współrzędnych prostokątnych do biegunowych).

808. Obliczyć całkę podwójną I — Jf g sin 95 dgd<p, jeżeli obszarem D

D

jest:

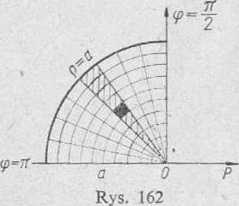
1)    wycinek kołowy, ograniczony liniami g = a, <p = te/2 i <p = n

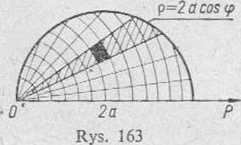
2)    półkole g ^ 2a cos <p, 0 < <p < ~

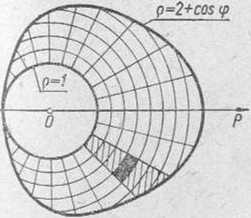
3)    figura płaska zawarta pomiędzy liniami g — 2-i-cosę> i g = 1 Rozwiązanie: 1) Okrąg g = a i promienie tworzące z osią biegunową kąty (p = n/2 iip — n ograniczają wycinek kołowy O AB o środku w biegunie O (rys. 162).

Całkując najpierw względem g, a potem względem <p, otrzymamy I— I sin<pd<p I gdg = j    sinrpdcp — ~ ( sinę-dcp — ~

*    0    n

T-    2    2

2) Przedstawiamy obszar D (rys. 163). Całkujemy, jak to się zwykle czyni we współrzędnych biegunowych, najpierw względem g, a potem względem cp

2acos<p

2

, 7 = J sin (pd<p | gdg = J

2<a cos

sin rpd(p —

— 2a¹ | cos² <73 sin yr/y = — 2a~ f (cos <p)²d(cos <p) =

~ł['

cos-*95

² 2

= -—-ar

3

3) Przedstawiamy obszar D (rys. 164). Całkujemy •

^2 ~U+cosę>

2.t    2+cos9>    2

sin <pd(p =

/ = ( sincpdcp |    <?</(? = J

Ó    1    0

2*

= -yj [(2+COS93)²— 1]sin92tfg? =    f (3+4coS9?-j-cos²9>)dcosrp —

o    2.1

=i{

3 cos<p+2cos²ęp4-

1    T

— cos³ 95    - 0

3    J2n

809. Całkę podwójną I = J J -^====-, gdzie D jest pierścieniem kołowym zawartym pomiędzy okręgami x*-ry² — 1 i x²Ą-y² = 4 (czyli 1 < x²+y² < 4, rys. 165), wyrazić we współrzędnych biegunowych, a następnie obliczyć.

Rys. 164

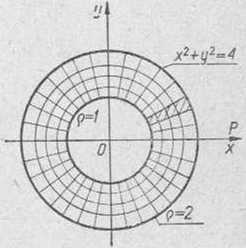
Rys. 165

Rozwiązanie. Posługując się podaną wyżej regułą, otrzymamy

2.-1

/- ff_—

I<e<2

Ke<2

d.' j/ p² cos² 95o² sin² 95 J “    •

Równania danych okręgów we współrzędnych biegunowych mają postać

e = 1 i 0 = 2.

810. Obliczyć całkę podwójną ff <fdcpdQ po obszarze Q ograniczonym:

Q

1)    okręgami q = a, q = 2a

2)    pierwszym zwojem spirali q = a<p i osią biegunową

3)    krzywą q = asin29?

341