171 2

335

9.4.Kodowanie tablicy przejść; problem wyścigów [4]

Kodowanie tablicy przejść polega, podobnie jak w układach synchronicznych, na przyporządkowaniu stanom wewnętrznym A stanów elementów pamięciowych Qj, Q->,...,Q^ . Elementarni pamięciowymi mogą być pętle sprzężenia zwrotnego albo przerzutniki proste (problem ten omówimy w rozaz. 9.5).

W celu zakodowania tablicy przejść o K wierszach (stanach wewnętrznych) należy przyjąć minimum k sygnałów dwustanowych, przy czym (por. (5.51)):

2^k_1 < K s 2^k    (9. 11)

Automat o K stanach wewnętrznych musi więc zawierać co najmniej k elementów pamięciowych.

Kodowanie automatów asynchronicznych jest procesem bardzo ważnym. Na skutek zjawiska zwanego wyścigami złe zakodowanie może spowodować złe działanie układu.

Zjawisko wyścigów może wystąpić w automacie asynchronicznym na skutek istnienia nierównych opóźnień w pętlach sprzężenia zwrotnego. Wyjaśnimy to na przykładzie.

Przykład 9,4

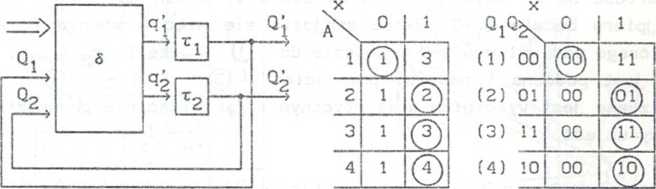
Rys. 9.5a przedstawia schemat blokowy automatu asynchronicznego z dwiema pętlami sprzężenia zwrotnego (por. rys. 9.8a). Załóżmy, że automat ten realizujący tablicę przejść z rys. 9.5b zakodowany został według rys. 9.5c. Dla jasności obserwacji założono, że całe opóźnienie układu kombinacyjnego S zostało wydzielone w torach sprzężeń zwrotnych (bloki Tj, T2 na rys. 9.5a).

Załóżmy, że automat jest w stanie stabilnym (T)    , tzn.. x=0,

Qj⁼Q2⁼0- Przyjmijmy, że w chwili tj sygnał wejściowy x zmieni się z 0 na 1. Zgodnie z tablicą przejść automat powinien przejść do stanu (5) zakodowanego jako 11, czyli oba sygnały sprzężenia zwrotnego Qj, powinny się zmienić z 0 na 1.

Jeżeli opóźnienia z^Zg, to ^autom.at zadziała prawidłowo. W chwili ^2 (nys. 9.5d) jednocześnie pojawią sie Qj⁼¹* i Q2⁼l- Praktycznie taki przypadek jest niemożliwy. Zawsze któreś z opóźnień będzie większe.

Jeżeli    > Tj , to będzie istniał przedział czasu, w którym Qj

zmieni już wartość na 1, a Q₂ jeszcze nie. Na wejściu układu 3 w chwili t₂ (rys. 9.Se) pojawi się zatem kombinacja x=l. <2^1, Q₂=0. Układ 3, zgodnie z tablicą przejść, wytworzy sygnały wyjściowe q₁ = l, q₂=0, co uniemożliwi zmianę sygnału Q₂ na 1. Ustalą się zatem wartości Ql=l, Q₂=0. czyli automat przejdzie do stanu @ zamiast do (3)

a)    b)    c)

d) .    e)

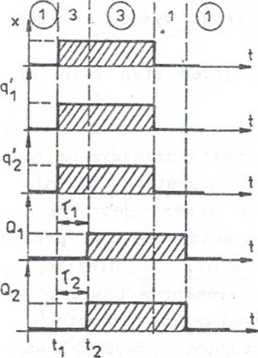
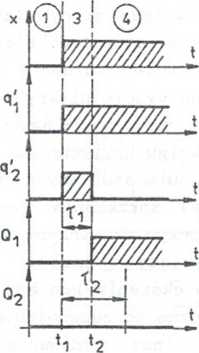
Rys. 9.5. Ilustracja zjawiska wyścigów krytycznych (przykład 9.4): a) schemat blokowy układu asynchronicznego z dwoma pętlami sprzężeri zwrotnych, b) tablica przejść, c) zakodowana tablica przejść, d) przebiegi czasowe przy założeniu Tj=t₂ ^^ez wyścigów), e) przebiegi czasowe przy założeniu f₁<r₂ (wyścig krytyczny)