19(4)

będzie się ślizgał coraz dalej. W przypadku skrajnym otrzymamy bardzo <j{ij niezwykle śliską powierzchnię, na której krqżek praktycznie nic zwalnia (ban? dobrym laboratoryjnym przybliżeniem takiej sytuacji jest ruch krążka nad duszce powietrznej, wytworzonej na poziomym stole z wieloma otworami, które wydmuchiwane jest powietrze).

Z tych obserwacji możemy wyciągnąć wniosek, ż.e jeśli na ciało nie dzi* żadna siła, to porusza się ono ze stałą prędkością. Otrzymujemy w ten spo$/ pierwszą zasadę dynamiki Newtona.

Pierwsza zasada dynamiki Newtona. Jeśli na ciało nic d/.inła żadna siła. to nic może zmienić się jego prędkość, czyli nic może ono przyspieszyć.

porusza, i<» będzie się nadal poruszać z tą samą prędkością (to /traczy z prędkością o tej samej wartości i kierunku).

5.3. Siła

Zdefiniujemy tera/ jednostkę siły. Wiemy juz. że siła jest pr/.yo/yną przyspieszenia ciała. Możemy zatem określić jednostkę siły za pomocą przyspieszenia, jakie nadaje ona pewnemu ciału wzorcowemu. W charakterze ciała wzorcowego użyjemy (a właściwie wyobrazimy sobie, że używamy) wzorca kilograma z. rysunku 1.4. Temu ciału przypisano — z definicji — masę równą dokładnie I kg.

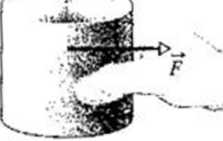
Rys. 5.1. Sita /'. działająca *nu wzorzec kilograma nadaje nm prz.yspjcs/enio a

Innymi słowy, jeśli ciało spoczywa, to pozostanie w spoczynku, a jeśli się

Umieśćmy ciało wzorcowe na poziomym stole bez tarcia i ciągnijmy je w prawo (rys. 5.1). Metodą prób i błędów możemy doprowadzić do tego, aby przyspieszenie ciała wynosiło 1 m/s'. Uznamy wtedy — na mocy definicji — żc

siła, jaką działamy na ciało, jest równa 1 niutonowi (oznaczanemu jako N ).

Możemy działać na nasze ciało wzorcowe siłą 2 N. nadając mu przyspic-

szenic 2 m/s*. ud. Mówiąc ogólnie, jeśli ciało wzorcowe o masie I kg uzyskuje

przyspieszenie o wartości a. to działa na nie siła o wartości (w niutonach) równej .

Tak wiec miara siły jest wywołane przez nia przyspieszenie. Przyspieszenie

liczbowo wartości jego przyspieszenia (w metrach na sekundę do kwadratu).

jest też. wielkością wektorową? Łatwo możemy przypisać sile kierunek (niech to będzie kierunek przyspieszenia), lec/ to jeszcze nie wystarczy. Musimy wykazać doświadczalnie, że siła jest istotnie wielkością wektorową. Dowód taki przepro-

wadzono — siły są wielkościami wektorowymi, a ich składanie podlega prawom algebry wektorowej z rozdziału 3.

Oznacza to, że gdy na ciało działają dwie lub więcej sił, ich siłę wypadkową otrzymujemy, dodając wektorowe poszczególne siły składowe. Jest to siła, której działanie na ciało jest takie samo, jak łączne działanie sił składowych. Właściwość ta nosi nazwę zasady superpozycji sił. Świat byłby bardzo dziwnie skonstruowany, gdyby w sytuacji, gdy na przykład ty i kolega ciągniecie ciało wzorcowe w tym samym kierunku siłą ł N każdy, siła wypadkowa wynosiła — powiedzmy — 14 N.

88    5. Sita i ruch I

ftej książce silę będziemy zwykle oznaczać jako F, a silę wypadkową k Podobnie, jak w przypadku innych wektorów silę. między innymi silę |ko^?wa, można rozłożyć na składowe wzdłuż osi układu współrzędnych. Gdy jjjc siły działają wzdłuż jednej osi, można opuścić strzałki nad symbolami l^ywać znaku do oznaczania kierunku sił wzdłuż lej osi.

(fożemy teraz zastąpić poprzednie sformułowanie pierwszej zasady dynamiki ona sformułowaniem, które jest bardziej poprawne, korzystając z pojęcia siły owej-

Lfwsza zasada dynamiki Newtona. Jeśli wypadkowa sił działających na ciało jest zeru (Fwyp — 0). to nic może zmienić się jego prędkość, czyli nic może ono "jnyspiewyć.

JjjLv

Ka ciało może działać wiele sił. ale jeśli ich wypadkowa wynosi zero, to dało nic doznaje przyspieszenia.

Inercjalne układy odniesienia

pierwsza zasada dynamiki Newtona nic obowiązuje we wszystkich układach odniesienia. ale zawsze można znaleźć laki układ, w którym zasada ta (podobnie jak cała mechanika klasyczna) jest słuszna. Takie układy nazywamy inercjalnymi układami odniesienia lub po prostu układami inercjalnymi.

^ Inercjalny układ odniesienia jest to taki układ, w którym spełnione są zasady dynamiki Newtona.

Na przykład, układ związany z Ziemią można uważać za inercjalny pod warunkiem, że zjawiska związane z astronomicznym ruchem Ziemi (jak jej ruch obrotowy) można pominąć.

Takie założenie jest usprawiedliwione, jeśli na przykład badamy ruch ślizgowy krążka na lodzie (bez tarcia) na krótkiej drodze — obserwator na Ziemi stwierdzi wówczas, że dla tego ruchu zasady mechaniki klasycznej są spełnione. Jeśli jednak będziemy badać ruch tego krążka na drodze bardzo długiej, powiedzmy od bieguna północnego do południowego, to obserwator na Ziemi stwierdzi, żc poruszając się na południc, krążek doznaje niewielkiego przyspieszenia w kierunku zachodnim (rys. 5.2a). Obserwator ton nie bodzie mógł jednak wykryć żadnej siły, powodującej to przyspieszenie. Układ /.wiązany z Ziemią jest w tym przypadku układem nicinercjalnynt, gdyż dla tego ruchu krążka nie można pominąć ruchu obrotowego Ziemi. Zaskakujące dla obserwatora przyspieszenie krążka, skierowane na zachód, jest bowiem spowodowane obrotem Ziemi pod krążkiem w kierunku na wschód (rys.rl 5.2b).

W lej książce będziemy zwykle zakładać, że układ związany z Ziemią jest inercjalny i żc to w nim dokonujemy pomiarów sił i przyspieszeń. Jeśli jednak takie pomiary będą wykonywane w układzie nieinercjalnym. na przykład w windzie poruszającej się ruchem przyspieszonym względem Ziemi, to ich wyniki mogą być nieoczekiwane z punktu wadzenia mechaniki klasycznej. Przekonamy się o tym m.in. w przykładzie 5.8.

N

w—j—n. s

»)

i

b)

Rys. 5.2. a) Długi tor krążka ślizgającego się bez tarcia po lodzie na południc, widziany przez obserwatora na Ziemi, b) Ziemia pod ślizgającym się na południe krążkiem przesuwa się nu wschód 7. powodu jej obrotu wokół własnej osi

5.3. Siła 89