210 211

210 Metody wielokryterialne

4.4.3. Metoda sumy ważonej

Kolejną możliwością generowania rozwiązań sprawnych jest uwzględnienie współczynników wagowych. Współczynniki le można interpretować jako wagi nadawane kolejnym kryteriom występującym w funkcji celu. Wartości współczynników wagowych można znormalizować tak, aby sumowaty się do jedności.

Przykład 4.6

Wykorzystując podejście sumy ważonej, należy znaleźć rozwiązanie zadania rozpatrywanego w przykładzie 4.2, odpowiadające decydentowi, który określił stosunek ważności kryteriów pierwszego do drugiego jako 3:1.

Przypomnijmy, że kryteria I i 2 mają, odpowiednio, postać:

y, =2x, +3x₂,

3^;2 — — 2x | — 2x₂.

Tworzymy nowe zadanie, w którym uwzględniamy podany przez decydenta stosunek ważności kryteriów, i otrzymujemy:

y = 3y, +y₂ = 3(2^1 + 3x₂) + (— 2x, — 2x₂) = 4x_t + 7x₂.

Powstaje w ten sposób zadanie programowania liniowego:

4jc, + 7x₂ —» max,

.Vj + 2x₂ ^ 8,

4x,    < 16,

X|, x₂ > 0.

Rysunek 4.10

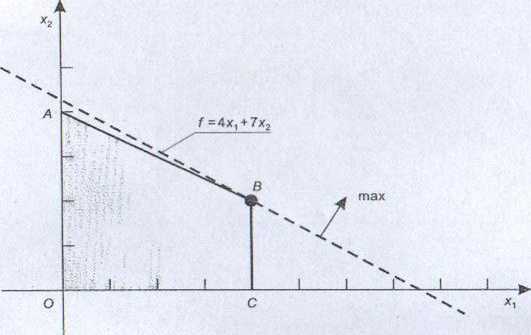
Generowanie rozwiązań sprawnych

21 I

Rozwiązanie geometryczne tego zadania jednokryterialnego w przestrzeni decyzyjnej przedstawiono na rys. 4.10.

Otrzymujemy punkt B, który jest zarazem rozwiązaniem sprawnym zadania wielokryterialnego.

4.4.4. Hierarchia kryteriów

Innym sposobem wyrażenia zróżnicowanego znaczenia dla decydenta rozpatrywanych w zadaniu celów jest wprowadzenie hierarchii celów. Hierarchizacja kryteriów polega na ustawieniu ich w takiej kolejności, aby kryterium najważniejszemu odpowiadał numer 1; pozostałe numerujemy w sposób ciągły. Dla każdej pary kryteriów ważniejszemu z nich przyporządkowany jest niższy numer. Rozwiązanie zadań hierarchicznych odbywa się sekwencyjnie. W pierwszym kroku znajdujemy rozwiązanie zadania jednokryterialnego, w którym jako kryterium przyjmujemy cel najważniejszy dla decydenta, natomiast zbiorem warunków ograniczających jest zbiór warunków ograniczających wyjściowego zadania wielokryterialnego. Następnie rozwiązujemy dalsze zadania jednokryterialne, uwzględniając cele zgodnie z. przyjętą hierarchią. Jako dodatkowy warunek ograniczający w zadaniu rozwiązywanym w kolejnym kroku dołączamy wymaganie, aby cel rozpatrywany poprzednio był osiągnięty na wyznaczonym w tym kroku poziomie. Tak więc w każdym kolejnym kroku liczba warunków ograniczających rozwiązywanego zadania zwiększa się o jeden.

Przykład 4.7

W zadaniu z przykładu 4.2 przyjmujemy następującą hierarchię: najważniejszy jest cel pierwszy, drngi w hierarchii jest cel drugi.

Jednokryterialne zadanie programowania liniowego dla pierwszego poziomu hierarchii ma postać:

2xi + 3x₂ —> max, x, +2x₂ < 8,

4xi < 16, x_h x₂ > 0.

Jego rozwiązaniem optymalnym jest punkt B, a optymalna w'artość funkcji celu jest równa 14 (jest to zadanie Z, z przykładu 4.4). Zadanie drugiego poziomu hierarchii ma postać:

-2x|-2x₂ —> max,

x, +2x₂ < 8,

4x, sg 16,

2X| + 3x₂= 14, x,, x₂ > 0.