216

Druga teoria zakłada, że pory mogą być koncentratorami naprężeń i mogą pełnić rolę defektów krytycznych. Teoria ta wiąże silnie zależność wytrzymałości z porowatością i dotyczy głównie dużych, przeważnie międzyziarnowych porów o dużej asymetrii. W ceramicznych materiałach budowlanych ich rolę pełnią głównie mikrospękania. Podstawową zależność, wynikającą ze zmodyfikowanego równania Griffitha, przedstawiono poniżej

<7 =

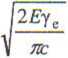
(3.95)

gdzie:

a - wytrzymałość na rozciąganie tworzywa, N/m²; y_c - wartość efektywnej energii pękania, N/m;

E - moduł sprężystości, N/m²;

2c    - wielkość defektu krytycznego, m.

Należy zwrócić uwagę, że zarówno moduł sprężystości E, jak i efektywna energia pękania y_e są funkcją porowatości. Można zatem powyższy wzór zapisać następująco

S_P =J 2

E₀e-^b*^Py_e0e~^aP

nc

(3.96)

gdzie:

E₀    -    moduł sprężystości ciała nieporowatego, N/m²;

Yco “ wartość efektywnej energii pękania ciała nie porowatego, J/m²; P    -    objętościowy udział porów;

bu, a    -    stałe;

2c    -    wielkość defektu krytycznego, m.

Energia pękania

Ogólnie można powiedzieć, że wielkość efektywnej energii pękania maleje wraz ze wzrostem porowatości tworzyw polikrystalicznych. Jedynie w przypadku materiałów zwartych, tzn. zawierających poniżej 5% porów, relacje te mogą być odwrócone. Natomiast dla ceramicznych materiałów budowlanych z dużym prawdopodobieństwem możemy przyjąć, że

YeP=Yeo*~^nP    (3.97)

gdzie:

Y_cp    -    energia    pękania ciała    porowatego, J/m²;

y_eo    -    energia    pękania ciała    nieporowatego,    J/m²;

P    -    objętościowy udział porów;

a    -    stała.

216