3(3)(1)

FUNDAMENTOWANIE II (KB IVr.)

Zestaw pytań oraz zadań do wykładu 3.

Pytanie 1.

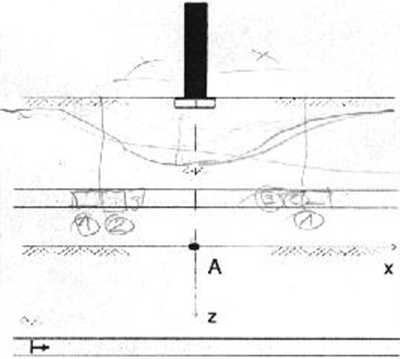
Zaproponować sposób wybrania całego pokładu (na zawał, bez pozostawiania filarów) w celu minimalizacji niekorzystnych wpływów deformacji terenu na wysoką zabytkową konstrukcję, która jest posadowiona na sztywnej płycie.

Przyjąć, że zadanie jest płaskie, jak na rysunku obok.

Wskazówka: który z parametrów deforacji terenu w, T, e. R jest tutaj najistotniejszy?

Pytanie 2.

Cały poziomy pokład będzie stopniowo wybierany z lewa na prawo (zadanie płaskie). Naszkicować tor, tj. trajektorię x(z), po której hipotetycznie będzie się poruszał osiadający reper A, w miarę postępu frontu eksploatacyjnego.

Pytanie 3.

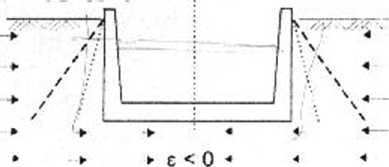
Długi żelbetowy zbiornik o poprzecznym przekroju 4m x 2m znajdzie się pod wpływem ściskających deformacji górniczych.

Ile razy wzrośnie moment zginający utwierdzenia ściany w płycie dennej, jeśli współczynnik parcia bocznego gruntu (niespoistego) wzrośnie od wartości spoczynkowej Ko = 0,5 do K_e = 1,5 *> Podać dwa proste sposoby ochrony ścian zbiornika od wewnątrz i od zewnątrz na czas wystąpienia deformacji górniczych.

Pytanie 4.

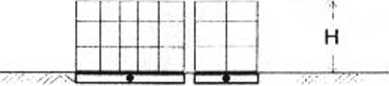
Pokazać przykład sytuacji, w której współczynnik eksploatacyjny dla osiadań górniczych a > 1.

Pytanie 5.

Czy deformacje górnicze terenu mogą być niebezpieczne dla fundamentu palowego?

1.1.11,1..,

Jy.W.^-.'-    ■ •*

Zadanie 1.

Nieskończenie długa belka o sztywności El na jednorodnym podłożu Winklera o stałej C osiadła równomiernie pod wpływem stałego obciążenia <\o Następnie na półosi x < 0 wystąpiło stałe osiadanie górnicze (próg) o uskoku S.

Na drugiej półosi x > 0 nie wystąpiło osiadanie górnicze Rozwiązać belkę.

i* I-i H •*' L2 ł

c

Zadanie 2.

Wyprowadzić wzór na minimalną obliczeniową szerokość szczeliny dylatacyjnej s dla odkształceń ściskających (so < 0) i równocześnie wklęsłej krzywizny (Ro < 0):

_L-h2±i

2

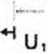
L - i

^U₂

£, + £,( U

—-- £₀ +-

2    1° R.-HJ

^L\ ⁺ L2 2

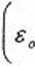
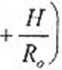
Zadanie 3.

Wyprowadzić wzór na promień graniczny dla belki o długości L na górniczym podłożu Winklera o stałej C_c

C₀I.²    1

! + </

Stosując wzór na korektę odporu podłoża Ao(x) z ćwiczeń projektowych.

Która krzywizna może wcześniej spowodować odrywanie tej samej ławy od podłoża:

Ro = +5,0 km (pod końcami ławy), czy Ro = -5,0 km (w środku ławy) ?

Wskazówka: warunek nieodrywania belki od podłoża oznacza, że naprężenia kontaktowe r(x) = q*, + óa(x) > 0