4539

104

Ukłdy równali liniowych

Dziewiąty tydzień - przykłady

105

Stąd wyniki, ic i s 2, y e 3, * = -1. c) W tym przykładzie mamy

12-30	0]		1 2	-3 0	0]
4 8-71	1		0 0	5 1	1
12-11	1	*J"*J	0 0	2 1	1
-1 1 4 6	0.	•|łW|	0 3	1 6	OJ

•« “*•*

*3-^w«

1 2	-3 0	0
0 3	1 6	0
0 0	2 1	1
0 0	S 1	1.

Rozwiązaniem tego układu równań aą liczby i = 1. y =* 0, z = 1, t = 0.1 * I Można przy tym zauważyć, że szukanie rozwiązania ze wzoru Cramcra byłoby bardzo pracochłonne. Również obliczenie macierzy odwrotnej wymagałoby większej ilości rachunków.

• Przykład 9.6

Rozwiązać podane układy Crainera „metodą kolumn jednostkowych":

-3

1

3

1

5

-3

1

3

®)

H)

Stądz = 4, y = -2₍x = 0,t = l.

0 0    0 -r

1	2	-3	0	0
		1				1	0	0	0	4
0	1	3	2	0		0	1	0	0	-2
0	0	i	1	1	“3 - -	0	0	i	0	0
. 0	0	0	2 1	2 1	«*l -3«*j 4	0	0	0	1	1

c)

2 x -    y + z = 1

-4* - 12y + * = 2 ;    b)

3* + 3y + z = 3

3r+y +5 +21 = 2 i -    y    +    3z    +    2s    =1

2* +    2y    +    z    +    s    +    31    = 3 .

i +    2y    -    z    -    s    +    t    = 1

y    +    2z    +    2s    =3

* +    y +    2z    +    31    =    1

3r -    y -    z    -    21    =    -4

2r +    3y -    z    -    i    s    -6 '

x +    2y +    3z    -    t    =    -4

d) Następny układ pięciu równali będziemy rozwiązywać ściśle według algorytmu Gaussa, dlatego nie będziemy zaznaczać wykonywanych operacji elementarnych. Dla przejrzysto* fci będziemy otaczać ramką ten fragment macierzy, który ulegnie zmianie w następnym kroki. Mamy zatem

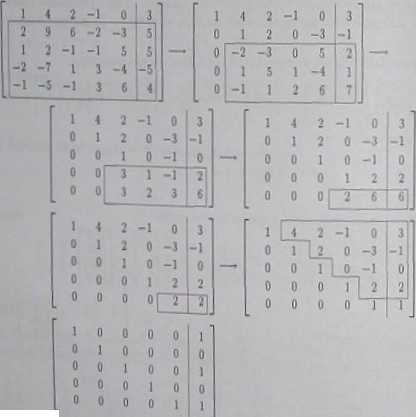
Rozwiązanie

.Metoda kolumn jednostkowych* jest praktyczną wersją metody eliminacji Gaussa. Po lega ona na odpowiednim przekształceniu macierzy rozszerzonej układu. W przypadku układów Cramera celem postępowania jest doprowadzenie wszystkich kolumn macierzy układu do postaci jednostkowej (t«n. z jedną jedynką i resztą zer) lak, aby jedynki w poszczególnych kolumnach znajdowały się w różnych wierszach. Dla układu Cramcra i n niewiadomymi metoda ta wymaga n kroków, gdyś w jednym kroku przekształca się ostatecznie całą kolumnę. Kolejność przekształcanych kolumn oraz położenie końcowych .jedynek” jest dowolna, przy czym praktycznie jest do przekształcenia wybierać kolumnę składającą się z jedynki, .małych" liczb całkowitych i -dużej" baby zer. W porównaniu z klasycznym algorytmem Gaussa metoda ta nie wymaga przestawiania wiemy ani budowania macierzy trójkątnej, wymaga jednak wykonania większej liczby mnożeń. Przekształcenie j-tąj kolumny. Chcąc w miejsce uiezerowtgo elementu a,, otrzymać Jedynkę", a na pozostałych miejscach j-tej kolumny same zeza wystarczy i-ty wiem macierzy rozszerzonej podzielić przei a,,. Następnie należy od pozostałych kolejnych wiemy odejmować i-ty wiersz mnożony odpowiednio przez a\_Jt są,..., •■-!;.    • ••.

a_R;. Schematycznie przedstawimy to poniżej

... «i, ...					■U	... 0 ...
... 0,-1; ...		1 ’	... fli-1; ... ... 1 ... ... fli+l; ...		»i-l -*i-l;“i	... 0 ... .. 1 ..
... O.j ... ... a.łl; ...					^u*fl	... 0 ...
.... ...			... On; ...	\	- "u;^0;	... 0 ...

n) Przekształcamy macierz rozszerzoną układu równań zaznaczając wyróżnione niczerowe elementy przekształconych kolumn oraz kolumny waeńniej przekształcone. Mamy

f 2 -1 1	1
-4 -12 1	2
l 3 3 1	3

T*ł

2 -1 liii -6 -U 0 1 1    4 0|2j

(0 -9 1 0 13 0