3cz2 zbiory

^U9rh 2> _te TT

1.43.    Załóżmy, że U = {1, 2, 3, 4, 5, 6, 7, 8, 9}. Potraktuj zbiór U jako przestrzeń ^ i wyznacz zbiory A, B\ A' u B', (A n B)', A' n B', (A w B)', jeśli:

a)    A = )x: x < 10 a x jest liczbą pierwszą}; B = jx x = 2k a x < 10 a k e N.}

b) A = {3, 6, 9); B = {1, 3, 5, 7, 9}

C) A = (x: x|8 a x e A/₊}; B - [x: x|6 a x e N₊}

1.44.    Wykaż, że dla dowolnych zbiorów A oraz B prawdziwe są równości:

a) {A w B)' = A' n B'    b) {A n B)' = A' u B’

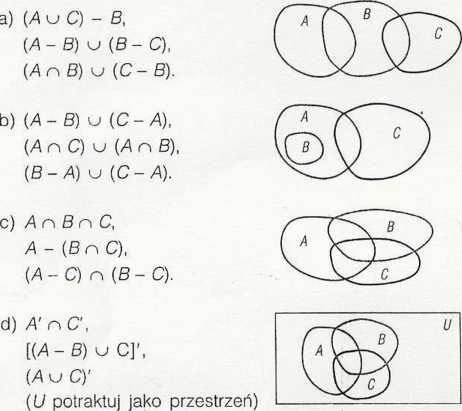
1.45. Na diagiamie poniżej dane są zbiory A, B i C. Na oddzielnych rysunkach zacieniaj podane zbiory:

*1.46. Aby dla dowolnych zbiorów A, B wykazać równość A-(A-B) = AnB możemy postąpić następująco:

Weźmy dowolny element x. Wówczas otrzymujemy:

x e A - {A - B) <=> x e A a x £ {A - B) <=> x e A a -i(x e A - B) o <=>    X e A a —i(x e A a x £ B) <z>    x e A    a    (x <e A v X e B) o

o    (x e A a X £ A) v (x e A a x e B) (x e    A    a xe A') v (x e A n B)    <=>

o    xeAnA'vxeAnB <=> xe0 v    X e A r    B    o xe0u(An8) <=>

«■ x e A n B

Zatem, dla dowolnych zbiorów A i B równość A-(A-B) = An8 jest prawdziwa. Udowodnij podobnie (korzystając z odpowiednich definicji działań na zbiorach oraz praw logiki) równość zbiorów:

a) {A u B) n (A n B) = A n B

b) (A u B) - {A n B) = (A - B) u (B - A)

c)    (A u B) - A = B - {A n B)

*1.47. Aby dla dowolnych zbiorów A, B udowodnić równość A u (A n B) = A, możemy wykazać, że dla dowolnego x, prawdziwa jest równoważność:

[x g A v (x G A A x g B)] <=> x G A.

W tym celu wystarczy uzasadnić, że wyrażenie [p v (p a q)] o p jest tautologią, gdzie p: x e A, zaś q: x e B.

Posłużmy się metodą zerojedynkową:

p	q	p A q	P v (p a q)	pv(pAg)op
1	1	1	1	1
1	0	0	1	1
0	1	0	0	1
- .^0 ..	0	0	0	1

Ponieważ wyrażenie rachunku zdań jest tautologią to równoważność jest prawdziwa, a co za tym idzie zachodzi równość A u {A n B) = A, dla dowolnych zbiorów A oraz B.

a)    W podobny sposób udowodnij, że dla dowolnych zbiorów A i B zachodzą równości:

1)    (A - B) u B = A u B

2)    A - B = A - (A n B)

3)    (A n S) u (A - S) = A

b)    W podobny sposób udowodnij, że dla dowolnych zbiorów A i B prawdą jest:

1)    (A c B) o (A n S = A)

2)    (BcA) <=> [(A' n 6'). = A']

3)    jeśli A' u B' = B' i A c B to A = B.

1.51. W klasie Ib jest 34 uczniów, wśród których: 24 umie jeździć na rowerze, 16 umie pływać, 10 umie jeździć na nartach; w tej liczbie 12 umie pływać i jeździć na rowerze, 5 umie jeździć na rowerze i na nartach, 3 umie pływać i jeździć na nartach. Dwie osoby w Ib uprawiają wszystkie wymienione dyscypliny sportowe.

a)    Ile osób w klasie Ib nie uprawia żadnej dyscypliny sportowej?

b)    Ile osób umie tylko jeździć na rowerze?

c)    Ile osób umie tylko pływać i jeździć na nartach?