anal0003

grupa

Egzamin z Analizy seml. (11.02.2004) imię i nazwisko ocena z zaliczenia

I    CUm, £ bt*' Ś a***    ^Cu<-'* mAA^ ^

^v'-Hh) Sformułować twierdzenie o trzech ciągach. Korzystając z tego twierdzenia udowodnić, że ze zbieżności do zera ciągu \a_n } i ograniczoności ciągu \b_n } wynika zbieżność do zera ciągu

\a_n b_n] Obliczyć lim

72—>00

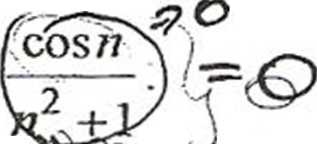
CoS (Y\^G <><(, 4>    CLu,*^— CL, * O

&C>

_    _w    /<- HjL Au, —!P

"1“ ■©Podać definicję różniczkrninkcji. Obliczyć wartość przybliżoną ar c tg 0.97.    ^    ¹

-(^-Sformułować i udowodnić podstawowe twierdzenie rachunku całkowego.    ^Od^-CULr

Obliczyć

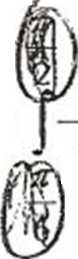
- 2 sin x

dx

ln² x

Jx

4. Znaleźć asymptoty funkcji /(x) =

5. Znaleźć ekstrema lokalne oraz punkty przegięcia funkcji /(x) = (x - 5)² • Jx

-    ' • f - • * ;    s r /

»:n.    % -    / Cv. f bu 4-

U/*—. ^

.•v*i    ^v -

- ■- a"'-'-.    jż>

'Cl

I

r.

• •• i

v

i V

• •

' y>

ć>.

D -

/

■> / ł- . -* -

-r_

• i

v».

OkC Cu,

II