Capture240

co zgadza się / wynikiem otrzymanym poprzednio, (idy |odn ,

mujc proporcje pół na pół. czyli gdy />,= </, = 0.50. wzór na ^C    |

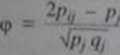
Gd> obie zmienne przyjmują proporcje pół na pół. czyli gdy _P -= 0.50. wzór ten przyjmuje postać:    '* ~P>^S f J

<p = 4/>,. - I.

Współczynnik fi jest powszechnie stosowany w d/icd/m,

etiologicznych. Zazwyczaj gdy badacze mówią o korelacji między " j , ujętymi pozycjami testu, mają na myśli współczynnik fi.

Współczynik li jest szczególnym przypadkiem współczynnika i, dług momentu iloczynowego (mieszanego). Jeżeli dwie kategorie <*., oznaczymy liczbami I i .6 i obliczymy w zwykły sposób współczynnik , momentu mieszanego, wynik będzie identyczny z <p.

Najmniejsza wartość współczynnika fi wynosi -I przy zwią/ku «k.ą mnym i +1 przy związku doskonale dodatnim. Jednak te wartości gran!./-.-' czynnik może przyjmować tylko wówczas, gdy obie zmienne maja p_f na pół. czyli gdy p, = q, - p, = q, - 0.50. Gdy obie zmienne maja ten 4 i • czyli p, = p, i </, = q_}. lecz są asymetryczne, czyli p, * _tj , _Pi .    , '

współczynnik fi może przyjąć jedną z wartości granicznych, ale mc oh* v większą i najmniejszą wartość graniczną współczynnika ę> wyraźny -sumy brzegowe. Rozważmy następujące tabele 2x2:

♦	0	50	50 ♦	50	0
-	50	0	50	0	50

50

50

50    50

50    50

3

4

—	♦		—	♦
20	60	80	40	40
20	0	20	0	20
40	60		40	60

W tabelach I i 2 obie zmienne mają proporcje pół na pół. a im? czynnik li może przyjmować wartości +1 i -I. W tabeli 3 mamy najwi<K-żliwy związek dodatni, pr/.y ograniczeniach wynikających / sum brzcę • Współczynnik li wynosi tu 0.613. Tabela 4 przedstawia skrajny z.wlązek przy tych samych sumach brzegowych. Współczynnik fi wynosi tu

““ ^b'“"‘^w,c'‘ ^ri——

^ O *\c wpływ sum brzegowych m zakres «r«ui(a fi m«/« nr_A nr • - h ,*t«0W*W*^h tego wipółczynniku oka,* „<    w, w ,adnvmr»*

n* pdtttWttl® ‘»ⁿ •** *^W*^/ku ' ^    Jc/xh •**,,«* koccU po-

litujemy Jako miarę skuteczności przewidywań,*. u, dokładne przewidzeń,- _kir.

U*. J«óncj «^nicnnc» ⁰³ P'^xisLłWIC    Wt»no * kierunku dodatnim ak

, ujemnym. j«l możliwe tylko wówczas. gdy oh, mikbdy nuja ten *», kinaft , s* symetryczne. Jeżeli jedna zmienna ma rozkład iy<maJo>. a druga prokainy dokładne przewidywanie okazuje mc niemożliwe i (akt ten znajduje ud/.wiertiedk-me we współczynniku korelacji Dokładne przewidywanie w jednym tylko kierunku wymaga syrnelrycznodci rozkładów Współczynnik fi. aczkolwiek /alc/ny od vum brzegowych, jest miar^ skuteczności przewidywania Z tego punkiu widzenia odzwierciedla on dobrze zmniejszenie dokładności przewidywana, wynikające z braku zgodności między dwoma rozkładami hrzrgowymi

Ponieważ X^{i= <v}9'. istotność <? możemy badać. porównując wartość No / wartościami krytycznymi podanymi w tablicy chi-kwadrat przy I stopniu swobody Gdy df- 1. ma odchylenie normalne i wartości o .,\ mo/cmy porównywać / wartościami krytycznymi podanymi w tablicy krzywej normalnej. Przy p«»bieniniu prób z populacji, w której nie występują żadne związki między badanymi zmiennymi. rozkład «p powinien być w przybliżeniu normalny z błędem standardowym \/4Ń. Oczywiście ma tu zastosowanie wszystko to. co odnogi «ę do małych liczebności (/.ob. podrozdział 13.9). Rzecz jasna S me może być zbyt małe

23.4. Wzorce odpowiedzi

Odpowiedzi podane przez N osób badanych w poszczególnych pozycjach toni można uj4Ć w postaci tabeli o n wierszach i A’ kolumnach W tabeli takiej wpisujemy jedynki i zera. Takie uporządkowanie danych określamy jako wy>w odpowiedzi. Tabela 23.2 przedstawia przykładowy wzorzec odpowiedzi podanych przez próbę 10 osób w teście składającym się z 5 pozycji.

Tabela 23.2. Wzonrcc odpowiedzi podanych pna p«*ę 10 «<* w \c*k składającym »ię z 5 pozycji

(boby

	1	2	3	4	5	6	7	8 9
1	n	"1	1		1	1		l 1
>	i	1	1	t		I	1
3	t	1		1	1	1	1
4	i	1	1	1
5	11	1	l		1
X	s	5	4	_3	3	3	2	J_L_

10 JS

I    o.so

0.60 0.60 a-w

0.40

I X = 2J?

Stopień trudności pozycp testu uwtdoaninoy ^    “** Z

niki w ostatnim wierszu. Średni wynik .? wynosi

477