CCF20090120080

PRZYKŁADY

1.    Sporządź następujące wykresy.

1} y = 2x;    2) y = 2x+l;    3) y = 2x+2;

4) y = 5- - ar.

Co możesz o nich powiedzieć? Jak opisałtayć słowami figury, -które one tworzą?

2.    Podobnie jak w przykładzie 1, sporządź następujące wykresy i opisz je.

l)y-3x;    2)y = Sar+i;    3) y = 3x+2;

4) y = 4- | ar.

3.    Co spostrzegasz, jeżeli chodzi o dwa następujące wykresy?

1) y — x²+'2x;    2) y — x²+4x+3.

i. Sporządź wykres y = ar(9—ar). Dla jakiej wartości x przyjmuje y wartość największą i jaka jest ta największa wartość?

5. Co spostrzegasz, jeżeli chodzi o następujące wykresy?

X) y = 25—x²;    2) y — x².

Liczby ujemne na wykresach, Często chcemy sporządzić wykres, w którego części x albo y, albo zarówno x, jak i y są ujemne. Możemy np. chcieć sporządzić wykres ukazujący długość szyny kolejowej przy temperaturach ujemnych. Jeżeli x oznacza temperaturę, to x ma być liczbą ujemną. Jeżeli na naszym wykresie x=X znajduje się w odległości centymetra na prawo od zera, to x — —1 będzie znajdować się centymetr na lewo, x — —2 znajdzie się 2 centymetry na lewo itd.

Podobnie, jeżeli y =1 znajduje się w odległości centymetra w górę od zera, to y — —.1 będzie znajdować się 1 cm w dół.

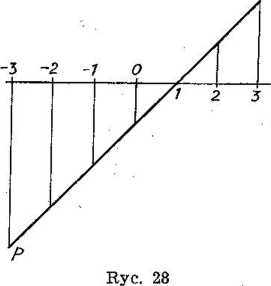
Sporządźmy dla przykładu wykres wzoru y = x—1 dla wartości x leżących pomiędzy —3 i 3. Zróbmy najpierw tabelkę:

X    —:3    —2 —ii 0    1    '2    <3

y    -4    -3 1—12    —1    iOi    1    2

Wartości x zaznaczamy na prostej poziomej. x — 3 zaznaczone jest w odległości 3 cm na prawo od zera, x = —3 w odległości 3 cm na lewo od zera itd. Odpowiednie wartości y przedstawione są przez odcinki pionowe. Gdy x — 3, to y — 2, tak ie z punktu, w którym znaznaczone jest x — 3, prowadzimy w górę odcinek o wysokości 2 cm. Gdy x = — 3, to y — —4, tak że z punktu, w którym znaznaczono x — — 3, prowa-162

dzimy w dół odcinek o długości 4 cm. Końce tych odcinków dają nam odcinek PQ, który jest żądanym wykresem wzoru y=x—l.

Q

Jedna z korzyści stosowania liczb ujemnych stanie się widoczna w przykładach dotyczących kształtu mostów. Bardzo często wzór jest znacznie prostszy, gdy przyjmujemy x —10 .w środku mostu, niż gdybyśmy przyjęli x — 0 na końcu mostu.

6.    Sporządź wykres funkcji y = x—2 dla wartości x zawartych pomiędzy 2 i 6.

Otrzymamy odcinek linii prostej. Przedłuż za pomocą linijki tę prostą w kierunku ^południowo-zachodnim”. Sprawdź, że ta prosta przechodzi przez punkty zawarte w tabelce dla wartości x pomiędzy —4 i 2;.

7.    Sporządź wykresy y — 5—x dla wartości x zawartych między -0 i 5. Otrzymamy odcinek prostej. Przedłuż tę prostą za pomocą linijki. Odczytaj wartości y odpowiadające wartościom x = 6 i x = 7. Dla jakich wartości x otrzymamy y równe 6 i 7? Czy to się zgadza ze sposobem znajdowania 5—(—1) i 5—(—2), wyjaśnionym w rozdz. 5?

8.    Wykresy opisujące kształty mostów. W książce R. B. Waya i N. D. Greena Building with Steel podane są szkice słynnych mostów. Pokazane tam krzywe przypominają wykresy .podanych niżej wzorów.

a) Wiadukt Langwies, Szwajcaria.

Przęsło centralne ize wzmocnionego betonu jest podobne do krzywej:

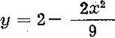
u*

163