CCF20091206014

Ponieważ E_k2 = 0, E_p3 — 0, więc E_k3 = E_p2 = 1569,6 kJ. Prędkość windy w stanie 3

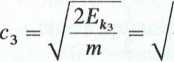
2-1569,6-10³ 2000

= 39,62 m/s

e)    Ponieważ winda zatrzymuje się na dnie szybu w stanie 4, zarówno jej energia potencjalna, jak i kinetyczna równają się zeru. Cała jej poprzednia energia E_k3 = E_p3 = 1569,6 kJ zostaje pochłonięta przez sprężynę.

f)    Jeśli układ termodynamiczny składa się z windy i sprężyny, to jego energia początkowa jest równa energii potencjalnej windy, czyli E_pi = 156,96 kJ. Energia całkowita układu może ulec zmianie tylko wtedy, gdy zachodzi wymiana energii między układem a otoczeniem. Podczas podnoszenia windy do układu zostaje doprowadzona (z zewnątrz) praca wynosząca L_x 2 = 1412,64 kJ. Stąd energia układu, w chwili gdy winda osiąga swe najwyższe położenie, wynosi 156,96 + + 1412,64 = 1569,6 kJ. Dalsze zmiany zachodzą wyłącznie wewnątrz układu, bez wymiany energii z otoczeniem. Tak więc energia całkowita układu pozostaje stała i wynosi 1569,6 kJ. Występują jedynie zmiany postaci energii z energii potencjalnej windy na jej energię kinetyczną, a następnie na energię potencjalną sprężyny.

Przykład 2.4. Kierowca samochodu o masie 1500 kg, zjeżdżając ze wzniesienia, widzi na dnie doliny czerwone światło, przed którym musi się zatrzymać. Prędkość samochodu tuż przed uruchomieniem hamulców wynosi 90 km/h, a wysokość wzniesienia w tym miejscu względem dna doliny — 50 m. Jaka ilość energii cieplnej musi być rozproszona przez hamulce, jeśli pominie się wpływ wiatru i innych oporów ruchu (opory toczenia itd.)?

Rozwiązanie

Dla samochodu jako układu termodynamicznego pierwsza zasada termodynamiki ma postać

AE = Q-L

Zmiana energii całkowitej AE składa się z dwóch części: zmiany energii kinetycznej AE_k i potencjalnej AE_p samochodu

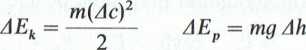
........ waż założyliśmy, że na granicy układu (nawierzchnia drogi

I współpracujące z nią koła samochodu) nie działają żadne siły, więc I U. i równanie bilansu energii redukuje się do postaci

+ mg Ah

m(Ac)²

1~

■' .iliin

+ 1500-9,81 (0-50) =

468 750 J-735750 J = -468,75 kJ-735,75 kJ = -1204,5 kJ

i ■. I pamiętamy, znak minus oznacza, że ciepło musi zostać oddane przez nH.iiI do otoczenia.

/wdania

/ Milanie 2.1. Obliczyć pracę w układzie zamkniętym, którego energia ".■wnętrzna uległa zmianie od wartości (7, = 3000 kJ do wartości l ,    2000 kJ, jeśli z zewnątrz zostało doprowadzone ciepło

(J, J = 4000 kJ.

Odp. L_u2 = 5000 kJ

/mianie 2.2. W układzie zamkniętym o energii wewnętrznej (7, = 400 kJ /ostała wykonana praca bezwzględna L_{l 2} = 100 kJ. Obliczyć energię wewnętrzną układu po przemianie, jeśli doprowadzono do niego ciepło w ilości <21,2 ⁼ 200 kJ. t >dp. U₂ = 500 kJ

/.udanie 2.3. Pompa działająca bez strat dostarcza wodę do wodotrysku. 1’rędkość wody na wylocie z dyszy wynosi 15 m/s. Obliczyć wysokość h, nu jaką wytryska woda.

Odp. h — 11,47 m

/mianie 2.4. Skrzynia o masie 500 kg zsuwa się po równi pochyłej. (idy składowa pionowa przebytej drogi wynosi 4,9 m, prędkość skrzyni

43