CCI20101006006

---------. .t«0fe9rt> .    -

»> Wykład z fizyki <«.

Pochodna funkcji w danym punkcie jest równa tangensowi kata nachylenia stycznej do wykresu funkcji w tym punkcie do osi x.

dx - różniczka argumentu x dy=y’dx - różniczka funkcji y=f(x)

dv

Wyraz ^ nazywamy pierwszą pochodną funkcji y względem x. Różniczkując pierwszą pochodną względem x otrzymujemy drugą pochodną funkcji

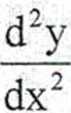
W analogiczny sposób można uzyskać wyższe pochodne.

Można obrazowo stwierdzić, że wartość pochodnej funkcji w danym punkcie wyraża intensywność, z jaka przyrasta wartość v funkcji w odpowiedzi na niewielka zmianę argumentu x funkcji w sąsiedztwie współrzędnej x_n danego punktu.

»> Wykład z fizyki «<

2.3.1 Podstawowe wzory rachunku różniczkowego

Jeśli u i v są funkcjami tego samego argumentu x, wówczas

(u +v)'= u'+v' (u- v)'= u'-v'

(u-v)'=u'-v + u-v'

fu\

w

u'v-u-v'

dz _ dz dy

Jeśli ^z = ^f(>0 oraz y^{= f}(^x) to    d_x ” dy dx

Przykładowe pochodne funkcji elementarnych:

— (a) = 0	— (x")=n-x^n-'	— (a^x)=a^xlna	— (sinx) = cosx
dx ^V	dx^v ’	dx' ’	dx^v ;
— (x)=l	— (e^x)=e^x	d /, \ 1 — (lnx) = —	— (cosx) = -sinx
dx ^v ’	dx^v '	dx ^ x	dx^v

6