2

94

VI. Pochodne funkcji postaci y—J (r)

Zachodzą twierdzenia:

(6.1.1) Jeżeli funkcja ma w danym punkcie pochodną skończoną, czyli jest funkcją

różniczkowalną. to jest w tym punkcie ciągła.

Ale funkcja ciągła może nic mieć pochodnej, np. funkcja >•= '.t| w punkcie x=0 (rys. 6.2).

(6.1.2)    Pochodna funkcji stałej równa się zeru, tzn. jeżeli y — C, to y - 0.

(6.1.3)    Pochodna iloczynu stałej przez funkcję równa się iloczynowi stałej przez pochodną funkcji, tzn. jeżeli y-c-f (x), to

y-c-f(x).

Niech u —f (x), u-g(x) oznaczają funkcje różniczkowalnc. Wówczas zachodzą trzy podane niżej wzory:

(6.1.4) Pochodna Sumy funkcji. Jeżeli _r — u +v, 10

y‘ =u' +v'.

(6.1.5) Pochodna iloczynu funkcji. Jeżeli y-uo, to

y'-uv I uv .

(6 1 61    Pochodna ilorazu funkcji. Jeżeli y - u Jo i o / 0, to

u v— uv

< 6.1.7) Pochodna funkcji złożonej (por. $ 4.3). Jeżeli funkcja złożona (superponowana) V =/(£<») jest określona w pewnym otoczeniu ptmkfu x-x_t>. funkcja g(x) jest różniczkowo i ruz w punkcie x-x_n, a funkcja f(u) różniczkowafna w punkcie u-u^. gdzie u₀~g(x₀), SO pochodna funkcji złożonej y f{g(x)) w punkcie x-x₀ obliczamy podług wzoru

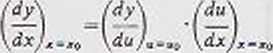
(6.J.S) Pochodna funkcji odwrotnej (por. § 4.5). Jeżeli funkcja różniczkowalną y—f(x) ma funkcję odwrotną x- v(y). to pochodna funkcji odwrotnej x = <p(y) równa się odwrotności pochodnej danej funkcji y-f (x):

Po prawej stronie wzoru po obliczeniu pochodnej dyjdx należy podstawić x = y(y). Przvklao. Dana jest funkcja y-Xg.se, której pochodna jest

dy 1 dx cos x