058 2

114 VI. Pochodne funkcji postaci y=f(x)

6.75. y 6.77. y

6.79. y 6.81. y 6.83. u 6.85. v 6.87. y 6.89. z

6.91.    u

6.92.    y

6.93.    v.

6.95. y 6.97. s: 6.99. s =

6.101. i

6.103. ;

6.76.

6.78.

6.80.

6.82.

z = \lax²+bx+c.

1

'JT+v—'JT—v

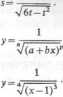
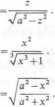
3 Jx

= MUłv, gdzie w, y, w są funkcjami róźniczkowalnymi zmiennej x.

= cos — , a#0.    6.94. x = asinbf.

a

— a sm —.

sin²3f.

1

cos⁴f'

sinf+cosf

2sin2f

xsinx l+tgx '

6.96. z=2x+sin2x.

6.98. u=4 cos⁵\t.

6.100.

5

6.102. z

sina a a 'sina

6.105. y=cosx-jc<	3S^3X.	6.106. >>= 5 sin^3x— f sin^5x+ $
6.107. y=tg*yfx.		6.108. y = 3ctgx+ctg^3x.
6.109. j’ = e“(asinx	-cosx).	6.110. y=x^2e^2xsmx.
6.111. y=cos^1J^		6.112. y=2sm^3J^-.
sin^2x ń 113. v =-=---	2	3cos^2x 6.114. v=——=—

6.115. y=Jsmx+\jx+2y/x.    6.116. y=Jl+tg^x +j

3 tg u — tg^3 u 6.117. ^z= 1—7T"ż— ' l-3tg ^Łu	6.118. z = tgu-ctgw-2u.
6.119. y=(4sinx — 8 sin^3 x) cos x.
6.120. y=arctg 3x.	6.121. 3' = 7arctg|x.
6.122. x=arcsin(l-t).	6.123. x = arccos y/l-t^2.
6.124. x = arcsin\/t^3.	6.125. x = aresin ~ .
6.126. y=aresin x+arcsinVl—x^2.	, 0<x<l.
6.127. x=arcsin2<Vl-t^2.	6.128. y = arctg (x—Vx^2 +1).
	6.130. >> = xarctgx-lln(x^2+l).
6.131. y=Ix^5arctgx-^x^4+^x^2	-^ln(l+x^2).
6.132. y = aresin ■ —.. Vl+x^2	6.133. y = arccos /i—— ■ Vl+x^2
6.134. y = arctg l^1~^xV l+x'	l+x 6.135. y=arctg-, x #1. 1 —X
(Lite „ _____ ^x	VT+?-i
i+Vi+*^2	X
«.!« j- ^aretg2lc . arcctg 2x	/l—aresin y 6.139. z= /--— ■ V 1 +aresin .y