063 2

124

VI. Pochodne funkcji postaci y=f(x)

6.3. RÓŻNICZKOWANIE GRAFICZNE

(O

w

dyjd_x

(7-1.1)

Dany jest wykres funkcji y=f(x) różniczkowalnej dla a^x^b. Znaleźć konstr& cyjnie wykres pochodnej y'=f'(x). Korzystamy z geometrycznej interpretacji pochody' (por. § 6.1, str. 93).

Metoda wykreślania jest następująca (rys. 6.11):

1° Dzielimy wykres danej funkcji na luki możliwie zbliżone do odcinków; otrzymujemy na osi Ox przedziały częściowe (niekoniecznie równe) o kolejnych końcach a_y, a₂,... _a

2° Kreślimy rzędne A_t M_t punktów M_it których odcięte są środkami przedział częściowych (a_t, a_i+1).

3° W punktach M_t prowadzimy styczne do odpowiednich łuków; będą one w p_rZy. bliżeniu równoległe do cięciw.

4° Z punktu S(—1,0), zwanego biegunem, wykreślamy równoległe do stycznych w punktach M_t wykresu danej funkcji y=f(x).

5° Otrzymane na osi Oy rzędne OR_t punktów przecięcia tych prostych z osią Oy wyznaczają odpowiednie wartości pochodnej.

6° Każdy z odcinków OR_t przenosimy równolegle wzdłuż osi Ox w ten sposób, aby punkt O pokrył się z punktem A_{. Wówczas drugi koniec R_t przesuniętego odcinka wyznaczy nam punkt P_f, należący do wykresu funkcji pochodnej.

7° Za pomocą krzywika łączymy otrzymane punkty P,.

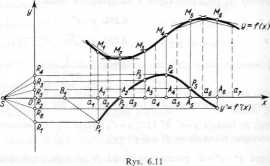
Istotnie, otrzymana krzywa przedstawia wykres pochodnej y'—f(^x) funkcji y f$' gdyż każde

/ł.P^OP.— SOtga—l tga—yj,

gdzie a, jest kątem, jaki tworzy styczna do wykresu funkcji w punkcie Mi z dodatni"¹ zwrotem osi Ox.

Rozdział VII

POCHODNE FUNKCJI OKREŚLONEJ RÓWNANIAMI PARAMETRYCZNYMI

§ 7.1. POCHODNA RZĘDU PIERWSZEGO

Jeżeli x i y są funkcjami ciągłymi tej samej zmiennej V.

*-/(»). y=g( 0, gdzie t przybiera wartości z pewnego przedziału, to mówimy, że funkcje te określają krzywą na płaszczyźnie. Zmienna t nazywa się parametrem. Na przykład gdy t oznacza czas, to równania (l).są równaniami ruchu punktu zakreślającego pewną krzywą. O krzywej tej mówimy, że równania (1) są równaniami parametrycznymi tej krzywej.

Różne równania parametryczne mogą przedstawiać tę samą krzywą (tzn. punkt ruchomy może poruszać się po tej samej krzywej w różny sposób). Parametr można rozumieć niekoniecznie jako czas, np. w niektórych zadaniach parametr ma znaczenie geometryczne (kąt, odcinek).

Krzywa (lub jej łuk) może być traktowana jako wykres pewnej funkcji y=h (x), gdy każda prosta równoległa do osi Oy ma z nią co najwyżej jeden punkt wspólny. W takim Przypadku równania x=f(t), y=g{t) określają również y jako funkcję zmiennej x. Ma •o miejsce np., gdy funkcja x=f(t) jest w przedziale a^t^b rosnąca lub malejąca, a tym ^samym i odwracalna (por. §4.5). Wtedy t = F(x), gdzie F oznacza funkcję odwrotną względem funkcji /, i równania (1) dają

y=g(F(x)).

Przypadku gdy istnieją pochodne /'(O i g'(i)< mamy wzory na obliczenie pochodnej lej funkcji bez potrzeby znajdowania funkcji odwrotnej F, mianowicie:

dy

dy dt dx dx ’ dt

dx _n dt

jeśli

Zad,

'Anie 7.1. Obliczyć pochodną dyjdx funkcji określonej równaniami parametrycznymi

x=sin t-tcost, y=cost+tsint.