053 2

105

]04    VI. Pochodne funkcji postaci y=f(x)

Zadanie 6.25. Zależność drogi s od czasu t w pewnym ruchu prostoliniowym dan_a jest równaniem s=/²-2f-8. Wyznaczyć prędkość średnią od chwili Ij=4 do chwjjj t_z=Ą+h, a następnie prędkość w chwili /1 =4.

Rozwiązanie. Droga przebyta w czasie od t_l do t₂ wynosi

zJs = s(f₂) —s(ti)=(4+/j)^z —2(4+fi)-8 —(4² —2 ■ 4-8) = /t²+6/t.

Prędkość średnia dla 4<t<4+h jest równa

As h² +6/i

zatem prędkość w chwili t=4 wynosi

p(4)=lim — = lim(h +6) = 6. a-o h A-O

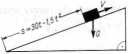
Zadanie 6.26. Dane jest równanie ruchu ciała wznoszącego się po równi pochyłej (rys. 6.4): s=30f-1,5/², gdzie 5 oznacza drogę przebytą w ciągu czasu t. Znaleźć: a) prędkość średnią ciała od chwili t=t₀ do chwili t = t₀+At; b) prędkość w chwili t=t₀; c) prędkość w chwili t=2 i w chwili 1=8; d) czas t, po upływie którego ciało będzie miało prędkość równą zeru.

Zadania

d) Prędkość spadnie do zera, gdy

u=30-3r=0, czyli z = 10.

Zadanie 6.27. Dla pewnego gazu, znajdującego się w gumowym zbiorniku, związek „oimędzy ciśnieniem p i objętością V wyraża się wzorem pV= 60. Znaleźć prędkość zmian lśnienia p w zależności od zmian objętości V dla V= 1 i dla V=2.

Rozwiązanie. Zmianie objętości AV odpowiada zmiana ciśnienia: Ap=p(V+AV)-p(V).

przyrost ciśnienia przypadający na jednostkę zmiany objętości zależy od objętości V j wyraża się wzorem

lim P(^v+dV)-p(l0 dp AV    dV '

60

A ponieważ p= —, więc

dp _    60

7y~~v²"

Prędkość zmian ciśnienia p w zależności od zmian objętości V wynosi

dp

dV

= -60

dla

V=l,

V=2.

= 30 —3l₀ —l,5/)t.

i w chwili r=8:

Rozwiązanie, a) Prędkość średnia dla t₀<l<t₀+At:

s(t₀+At)-s(t₀) 30t_o + 30At — l,5tl — 3t_oAt — 1.5At² — 30t_o + l,5to 30At — 3t_oAt — ],5Ar

b)    Prędkość w chwili t=t₀:

v(I,)- lim ^s<^l°+'^;,,)~^ł(1°⁾ ₌ lim (30- 3f„ -1,5 JO « 30 - 3!₀.

dt—0    At    At-0

c)    Prędkość w chwili t-2:

u(2) = 30 —3 -2=24 u(8) = 30 —3-8=6.

Zadanie 6.28. W obwodzie prądu nieustalonego o równaniu i=3te' ¹ + 1 znajduje się dławik o oporze czynnym 7?=0,2Q i indukcyjności Z,=0,01 H. Obliczyć wartość spadku napięcia

di

AU — Ri+L — dt

na dławiku w chwili t— 1.

Rozwiązanie. Obliczmy pochodną

di , .    , ,

—=3e^,_1+3fe'^_1=3(/ + l)e'"¹, dt

^a*ięc

AU = R(3te^,~¹ +l) + 3L(M-l)e^,-‘.

Dk , ,

¹ otrzymujemy AU=4R+6L=0,36.

Udanie 6.29. Ilość elektryczności q, jaka przepłynęła przez pewne urządzenie od ^chwj]j , „    da

‘-u, wyraża się wzorem q=2te . Wyznaczyć natężenie prądu /=- w chwili