6

98
VI. Pochodne funkcji postać: >•=/(*)
Rozwiązanie. Funkcja y jest ciągła, gdy x>0. Dzielimy licznik przez mianownik zastępując przedtem pierwiastki odpowiednimi potęgami o wykładnikach ułamkowych:
Obliczamy pochodną

Zadanie 6.6. Obliczyć pochodną funkcji
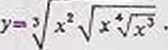
Rozwiązanie. Funkcja y jest ciągła, gdy .v£0. Zastępujemy pierwiastki potęgami o odpowiednich wykładnikach ułamkowych poczynając od najbardziej wewnętrznego pierwiastka:
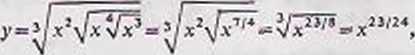
skąd

Zadanie 6.7. Obliczyć pochodną funkcji y = x’cosx. Rozwiązanie. Stosujemy wzór na pochodną iloczynu:
/ - (x3)' cos x+x3 (cos x)' = 3xJ cos x-x3 sin x -
Zadanie 6.8. Obliczyć pochodną funkcji
2—xł
V- ----
7 2x34-x+3
Rozwiązanie. Stosujemy wzór na pochodną ilorazu. Pochodna licznika (2-xi)'=» *» — 2x, pochodna mianownika (2xł+x+3)'=6xJ +1, a więc

Zadanie 6.9. Obliczyć pochodną funkcji
y » (4xs — 7xs + I4xł - S)3.
Rozwiązanie. Daną funkcję można uważać za funkcję złożoną: y=u\ gdzie u=4xł-7x3 + 14xI-S. Pochodną funkcji y względem x obliczamy podług wzoru (6.1.7):
dx du dx
dy dy du
*
Wyszukiwarka
Podobne podstrony:
063 2 124 VI. Pochodne funkcji postaci y=f(x) 6.3. RÓŻNICZKOWANIE GRAFICZNE (O w dyjdx (7-1.1) Dany
054 2 106 VI. Pochodne funkcji postaci y=/(x) Zadania 107 — 6e a więc Rozwiązanie. Mamy da i = — =
062 2 122 VI. Pochodne funkcji postaci >•=/(*) Rozwiązanie. Siła działająca na ciało o masie m wy
063 2 124 VI. Pochodne funkcji postaci y=f(x) 6.3. RÓŻNICZKOWANIE GRAFICZNE (O w dyjdx (7-1.1) Dany
100 VI. Pochodne funkcji postaci y—f(x) Zadanie 6.13. Obliciyć pochodną funkcji y=c~ . Rozwiązanie.
94 VI. Pochodne funkcji postaci y—J (r) Zachodzą twierdzenia: (6.1.1) Jeżeli funkcja ma w danym punk
049 3 96 VI. Pochodne funkcji postaci y=f(x) (6.1.15) (arcsinx) = -=L=, —1<x<1,
) VI. Pochodne funkcji postaci y=f(x) Zadanie 6.13. Obliczyć pochodną funkcji y=e~
053 2 105 ]04 VI. Pochodne funkcji postaci y=f(x) Zadanie 6.25. Zależność drogi s
056 3 110 VI. Pochodne funkcji postaci y=f(x) w czasie /, a y — drogę przebytą w tym czasie przez sa
058 2 114 VI. Pochodne funkcji postaci y=f(x) 6.75. y 6.77. y 6.79. y 6.81. y 6.83. u 6.85
059 2 116 VI. Pochodne funkcji postaci y=f(x) 6.140. }> = x3arctgx3. 1 acosx+b 6.143. y = —===.
060 3 VI. Pochodne funkcji postaci y=f(x) 6.209. Wykazać, że styczna do hiperboli
matma2 114 VI. Pochodne funkcji postaci y=f(x) 6.75. y 6.77. y 6.79. y 6.81. y 6.83. n 6.85. v&
matma3 116 VI. Pochodne funkcji postaci >•-/(.,) 6.140. y = x3arctgx3. 6.141. arcsin 4 y ”l
96 VI. Pochodne funkcji postaci >•-/(*) (6.1.15) (arcsinx) = , , — 1 < je< 1. —
więcej podobnych podstron