Cialkoskrypt!2

422 5. Jednorodny przepływ w kanałach otwartych

Średnia prędkość przepływu

1    2    i    i

V = —(R_h )ś Vs =-0,1855^0,002 =1,12 —.

n    0,013    s

Objętościowe natężenie przepływu

s

Q = A-V =0,295-1,12 = 0,33 —.

ZADANIE 5.4.8

W kanale otwartym o przekroju cylindrycznym, promieniu R = 50 cm i pochyleniu podłużnym 0,002 płynie woda. Strumień objętości (objętościowe natężenie przepływu) Q=0,1m³/s. Obliczyć głębokość wody w kanale, jeśli współczynnik Manninga jest równy 0,014 s/m^1/3.

Rozwiązanie

Do wyznaczenia nieznanej wartości kąta 0 zastosujemy iteracyjną metodę Newtona: 0_j+t =0.₍ -F(0_i)/F^/(0_i), i = 1,2,... Zatem na podstawie wzorów (5.30) i (5.31) otrzymujemy:

dF

de

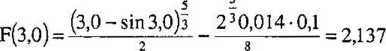
3,0³    0,5³A/0,002

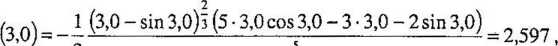
5

3,0³

stąd

■yj - - = 3,0—--= 2,177 rad =124,73°.

dF/o x    2,597

Ponieważ 0₂ > 90°, poziom wody znajduje się powyżej środka kanału cylindrycznego. Głębokość wody w kanale

H = R - R cos 0 = R (1 - cos 0) = 0,5 • (1 - cos 124,73°) = 0,5 • (l + 0,5698) = 0,785 m.

Ze względu na bardzo dużą szybkość zbieżności metody Newtona ograniczono się do jednej iteracji.

ZADANIA RÓŻNE

ZADANIE 6.1

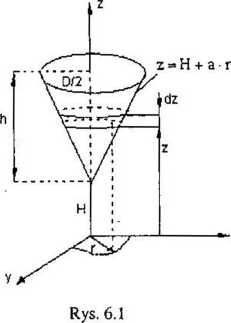
Wyznaczyć energię potencjalną cieczy o stałej gęstości p zawartej w zbiorniku o objętości V, którego wysokość wynosi h (rys. 6.1). Zbiornik jest umieszczony w odległości H nad płaszczyzną x - y. Obliczenia wykonać dla V = 100 000 m³, p = 1000 kg/m³, h =

20 m, H = 50 m i trzech kształtów zbiornika:

1)    w postaci paraboloidy obrotowej o równaniu z = H + a * r²,

2)    w postaci stożka kołowego o równaniu z = H + a • r,

3)    w postaci stożka ściętego o pobocz-nicy nachylonej pod kątem a = 45° do podstawy.

Rozwiązanie

Energia potencjalna warstwy cieczy o grubości dz

d<£> = dm-g‘Z = pdV -g-z = p • A(z)-dz-g-z, stąd całkowitą ilość energii potencjalnej zawartej w objętości V określa wzór:

= Jpg ■ z • dV = pg ■ Jz ■ dV .

v    v

Ponieważ środek ciężkości objętości V względem płaszczyzny x - y wyraża się wzorem:

_Zs=lj^z-dV,

V