DSC00313 2

Sprawdzian z podstaw robotyki

Wyniki obliczeń należy wpisać do tabeli z dokładnością do trzech cyfr po przecinku.

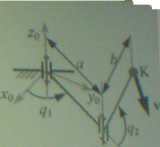
I. Rysunek przedstawia schemat kinematyczny manipulatora, jego wymiary oraz sposób odmierzania współrzędnych wewnętrznych. W rozpatrywanej chwili znana jest konfiguracja manipulatora oraz prędkość liniowa punktu K, wynosząca v^(0> = [v_x v_v v.]^T. Obliczyć prędkość wewnętrzną q₇.

Dane; a * 5 (m), b ~ 9 (m),    = 0.9 (rad), q₂ = 0.5 (rad), v, = 11 (m/s), v, = 7 (m/s).

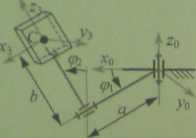
2. Manipulator przenosi obiekt o środku masy w punkcie C, masie m i macierzy bezwładności jf' W rozpatrywanej chwili znana jest konfiguracja manipulatora i jego prędkości wewnętrzne.

Obliczyć energię kinetyczną przenoszonego obiektu.

Dane: m - 5 (kg), (kg m²), a - 1.4 (m), b - 2.3 (m),

<Px = 7dA (rad), q>i~ idA (rad), 11 (rad/s), ^ - 7 (rad/s),

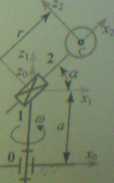
3. Manipulator przenosi jednorodną kulę o masie m i momencie bezwładności względem średnicy J. W rozpatrywanej chwili układy odniesienia Tio i fli mają jednakową orientację. Należy policzyć siłę F i moment M^<0\ zredukowane do początku układu no, jakimi podstawa 0 oddziałuje na człon 1, równoważąc obciążenie wywołane ruchem kuli. Do tabeli należy wpisać jedynie składową M_f momentu.

Dane: «*J (kg), J - 36 (kgm²), a*= nlA (rad), a =* 1.4 (m), Q)~ 5 (rad/s), oj ~ 10 (rad/s²), r ** 0.9 yjl (m), r - 3.6 yjl (m/s), r = 0 (m/s²).

Imię i nazwisko	q7 (rad/s)	BO)	M, (Nm) 1
	.cyn		5*2. «a|

0 0 2 0 0 1

(kgm²).