Egzamin v2

Egzamin / podstaw robotyki

Wyniki obliczeń należy wpisać do tabeli z dokładnością do trzech cyfr po przecinku.

l. Kysimek przedstawia schemat kinematyczny manipulatora oraz sposób odmierzania współrzędnych wewnętrznych. Należy obliczyć współrzędną q_h znając położenie punktu K i wiedząc, źe współrzędna <7? należy do przedziału <0, 7i>, a współrzędna q_:. przyjmuje wartości dodamie.

(0>

Dane: <?” 8 (dm). rJT = H2 8 161^T(dm).

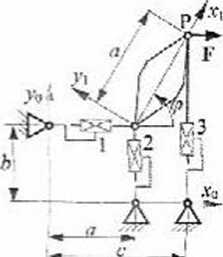
2. Z platformą ruchomą płaskiego manipulatora równoległego związany jest układ r.,, a z jego podstawa układ 7i_n. W rozpatrywanej chwili usytuowanie układu Kj względem a₀ opisane jest przez wektor rć? = [a ÓJ^T i kąt obrotu względnego <p. Platforma jest obciążona zewnętrzną siłą F^S| = [/■' 0J^T o linii działania przechodzącej przez punkt P. Należy obliczyć wartości sił napędowy ch równoważących przyłożony moment, do tabeli wpisując jedynie silę w parze postępowej numer 1.

Dane: a = 8 (m), h = 8 (m), c » 12 (m), <p= ,*3 (rad), F" 120 (N).

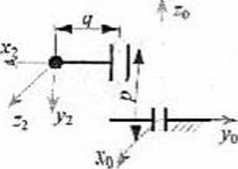
3. Z członami manipulatora o schemacie pokazanymi na rysunku związano zgodnie z regułą Denavita-Hartcnberga lokalne układy odniesienia. Cześć

parametrów D-H podano w tabelce,

pozostałe można odczytać z rysunku. Należy' obliczyć współrzędną x początku układu u* w układzie rto w chwili, gdy zmienne parametry przyjmują wartości 0, = 0.4 (rad) i & 0.8 (nul).

Dane: p = )7 (dm), q - 3f> (dm).

	' 4	d,	«	v, j
1	var		-q	1
2	var	0		rt2 1

4. Manipulator o dwóch parach obrotowych przenosi jednorodną kule o masie m i momencie bezwładności względem średnicy J. W rozpatrywanej chwili układy jt₀, i k₂ mają jednakową orientację. Należy' policzyć silę F°' i moment M^sl, zredukowane do początku układu jakimi podstawa 0 działa na człon \, rówoawatag,    wąrwołaiui    Q<n kakeJA wtf&aŁ uwncŁoA

Dąnę: a = 4 (m). b = 8 (m),    = 8 (kg), J = 32 (kg m²),

ft*i\ = 4 (rad's), m,- - 8 (rad/s), iy_u| =4 (rad/s²), ty,, = U (rad/s²).

0 .v_c

Imię i nazwisko	<7i (rad)	r 2 (Kł j x (dm)	M (N m)
	~J, ?4 7	-JO?*?óC | 0- a°o	33-04. Sfc