Kolokwium 1 i 2

Zadania przykładowe

Wyniki obliczeń należy wpisać do tabeli z dokładnością do trzech cyfr po przecinku.

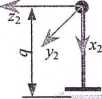
1. Człon o kształcie prostopadłościanu tworzy z podstawą parę sferyczną. Człon ustawiono tak, że krawędzie prostopadłościanu były równoległe do osi związanego z podstawą układu odniesienia 7i₀ o początku w środku pary sferycznej. Następnie dokonano obrotu o kąt a wokół osi x, a potem o kąt P wokół osi y układu 7i₀. Obliczyć wektor wodzący wierzchołka P w układzie 7t₀. Do tabeli wpisać jedynie współrzędną z tego wektora. Dane: k = 1 (cm), l = 2 (cm), m = 4 (cm), a= 5 (deg), /?= 20 (deg).

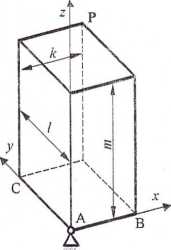
_Zo    2. Z członami manipulatora o schemacie pokazanym na rysunku związano

zgodnie z regułą Denavita-Hartenberga lokalne układy odniesienia. Część

parametrów D-H podano w tabelce, pozostałe

i	e,	di	ai
i	var		ą
2	var	P		0

można odczytać

z rysunku. Należy obliczyć współrzędną * początku układu n₂ w układzie jt₀ w chwili, gdy zmienne parametry przyjmują wartości 0\ = 10 (deg) i 02 = 20 (deg). Dane:p = 3 (dm), q =5 (dm).

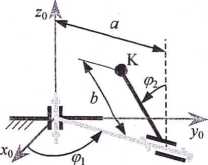
S/zy    ^Ry^sunek przedstawia schemat kinematyczny manipulatora, jego

' wymiary oraz sposób odmierzania współrzędnych wewnętrznych q>\ i qh- Współrzędne kartezjańskie punktu K oznaczono przez ,= \x y zj ■ Wartości x iy są zadane, należy obliczyć odpowiadające im kąty <pi i ^. Przyjąć, że

współrzędna qh przyjmuje wartości z przedziału [0, zr/2 j. Do tabeli należy wpisać tylko współrzędną Dane: a = 3 (dm), b = 2 (dm), x = -3 (dm), y = -1 (dm).

Imię i nazwisko	z (cm)	x (dm)	<P\ (deg)
	3.566	0.818	-143.130

4. Z platformą ruchomą pokazanego na rysunku manipulatora równoległego związany jest układ 7r_b a z jego podstawą układ 7t₀. Obliczyć długość siłownika /, kiedy usytuowanie układu 7ti względem 7t₀ opisane jest przez 2 0]^T (dm) i trzy kąty Eulera (zxz) a = 0.15 (rad), /? = rc/2 (rad), y= 0 (rad).

Dane: rf = [3 4 0]^T (dm), sil? = [5 6 0]^T (dm).

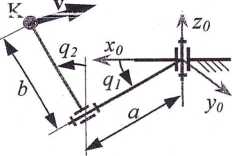
5. Rysunek przedstawia schemat kinematyczny manipulatora, jego wymiary oraz sposób odmierzania współrzędnych wewnętrznych. W rozpatrywanej chwili znana jest konfiguracja manipulatora i jego prędkości wewnętrzne. Obliczyć moduł prędkości liniowej punktu K względem podstawy.

Dane: a = 3 (m), b = 5 (m), q, = ntA (rad), q₂ = nlA (rad), q_x= A (rad/s), q₂ = 3 (rad/s).

6. Pokazany na rysunku człon o kształcie prostopadłościanu i jednorodnie rozłożonej masie obraca się z prędkością co wokół przekątnej OA. Należy obliczyć energię kinetyczną członu.

^: 20 (rad/s),

wektor ro? = [1

«=6(kg),J^<c^> =

= 0.6	(m), h	= 0.8
'0.25	0	0
0	0.17	0
0	0	0.10

(kg nr).

Imię i nazwisko	/(dm)	v (m/s)	BO)
	6.800	17.733	62.080