Finanse p stwa Wypych)0 291

Zarządzanie kapitałem obrotowym

terytorialnego zasięgu rynków ich zbytu, rodzaju kanałów dystrybucji, warunków sprzedaży, a także od wielu innych czynników.

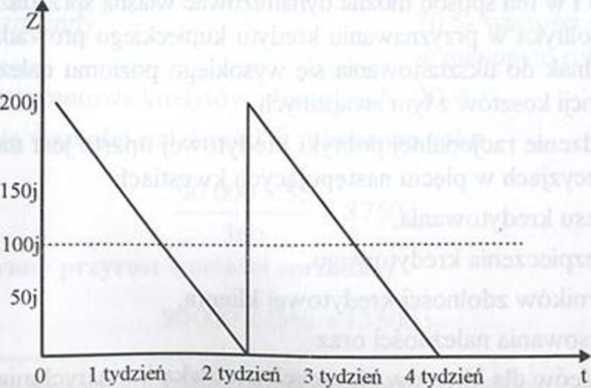
Zagadnienie zależności, o których mowa przedstawiamy przy pomocy rysunków 8.5. oraz 8.6. Przedstawiony na rysunku 8.5. model pokazuje jak kształtuje się poziom zapasu w momencie dostawy (na początku tygodnia najwyższy - 100 jednostek) i tuż przed następną dostawą (na końcu tygodnia - 0 jednostek). Rośnie on do poziomu maksymalnego (równego wielkości dostawy) w momencie dostawy aby każdego dnia zmniejszać się na skutek zużycia części zapasu w produkcji itd. Średni poziom miesięczny ukształtuje się w wysokości 50 jednostek. Jeśli zwiększy się dostawę jednostkową, co umożliwi oczywiście rzadsze dostawy, to jak widać z kolejnego rysunku średni poziom zapasów zwiększy się. W przykładzie kolejnym zwiększono poziom jednostkowej dostawy dwukrotnie zmniejszając oczywiście również dwukrotnie częstotliwość dostaw (z czterech do dwóch w miesiącu). Prezentuje to rysunek 8.6. Średni poziom zapasów w tym wariancie zwiększył się również dwukrotnie w ślad za wzrostem poziomu dostawy osiągając wysokość 100 jednostek.

Z przedstawionych modeli można wysunąć wniosek następujący: zwiększając poziom jednostkowej dostawy zwiększamy zarazem poziom zapasu. Model deterministyczny ma raczej dydaktyczne zastosowanie. W praktyce stosowany jest doskonalszy model -dwuskładnikowy. W deterministycznym modelu zapas zużywa się całkowicie zanim zostanie odnowiony. Jeśli jednak z wielu nieprzewidzianych a możliwych w praktyce przyczyn nastąpi opóźnienie dostawy to

Rysunek 8.5. Deterministyczny model zapasów (wariant I)

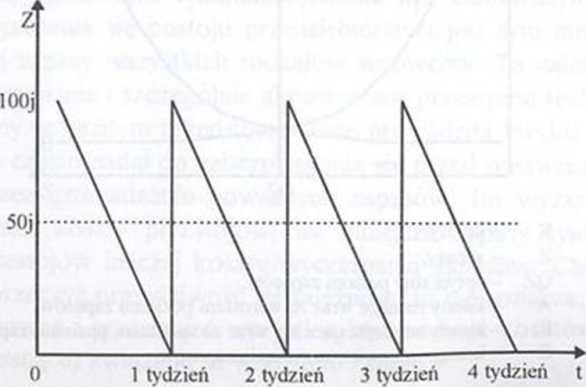
w przedsiębiorstwie wystąpi nieunikniona przerwa w produkcji, która jest zwykle bardzo kosztowna. Tę wadę eliminuje model dwuskładnikowy, w którym przewiduje się występowanie rezerwy minimalnej, która ma stanowić swoisty bufor przed opóźnieniem dostaw. Poziom tej rezerwy uzależniony jest od wielu przyczyn takich np. jak: dostępność danego surowca na rynku krajowym, monopolistyczny lub nie charakter dostaw, pochodzenie krajowe lub zagraniczne (bliskie lub dalekie jak np. kauczuk naturalny, asfalt), warunki transportu (np. specjalny nadzór nad ładunkami szkodliwymi dla życia lub zdrowia). Istotę modelu dwuskładnikowego prezentuje rysunek 8.7.

Rezerwa służąca ochronie przedsiębiorstwa przed postojem zwiększa trwale średni poziom zapasów (w wariancie III wynosi 100 jednostek a więc jest dwa razy wyższy niż w wariancie 1) co oznacza, że poziom rezerwy wymaga także racjonalnego podejścia. Im wyższa rezerwa tym pewniejsze zabezpieczenie przed postojem. Jednakże nie w każdym przypadku jej wielkość musi być równa całej dostawie. Może ona stanowić np. jej piątą lub dziesiątą część. O tym jednak trzeba już zdecydować w każdy przypadku rzeczywistego przedsiębiorstwa oddzielnie.

Rozumowanie tu przeprowadzone trzeba przeprowadzić dla każdego surowca oddzielnie. Jeśli uwzględnimy fakt, że w magazynach przedsiębiorstw występuje od kilkudziesięciu do kilkuset, a nawet kilku tysięcy pozycji magazynowych to wydaje się to niemożliwe.

W praktyce problem pracochłonności obliczeń łagodzony jest znacznie z dwóch powodów. Po pierwsze - kalkulację poziomu kosztów wystarczy przeprowadzić w stosunku do kilku lub kilkunastu

Rysunek 8.6. Deterministyczny model zapasów (wariant II)