Image57

112

W naszym przypadku

TU

co, =    [s"¹], (p = O, <r = 0,4, m² = 2,62 [s~²] i C = 6,7 • 10 ² [m]

Stąd otrzymujemy równanie ruchu punktu

x + 0,8 x -f 2,62 x = 0

i jego rozwiązanie

x = 6,7 * 10 ² e ^0M sin ~ £ [m].

TU

b. Z warunku sin ^ £ = sinc^t = 0 znajdujemy czasy, w których punkt znajduje się w położeniu równowagi w rozważanym przedziale [0, 27]

h = 0,

£₂ — 2 [s],

£3=4 [s],

U = ⁶ [s],

8 [s].

Z warunku

dx

dt

0 znajdujemy czas £^/1 = 0,84 [s], odpowiadający

pierwszemu maksimum lokalnemu funkcji x(£). Znając okres, znajdujemy stąd czasy odpowiadające kolejnym ekstremom lokalnym w rozważanym przedziale [0, 27]

t!₂ = 2,84 [s],

t'

4,84 [s],

t⁷* = 6,84 [s]

Podstawiając znalezione wartości t do równania ruchu otrzymujemy od powiadające im wartości wychylenia punktu. Na tej podstawie możemy sporzą dzić szukany wykres zależności x(£).

2.58. Równanie drgań kulki w cieczy ma postać

ÓTUT/r .    _

x + - x + ar x = 0,

m

gdzie x jest wychyleniem mierzonym względem położenia równowagi statycznej, r] jest współczynnikiem lepkości cieczy. Z teorii wiemy, że stały współczynnik

występujący przy prędkości ruchu jest równy podwójnemu współczynnikowi tłumienia drgań a, a ten wiąże się z częstością drgań związkiem

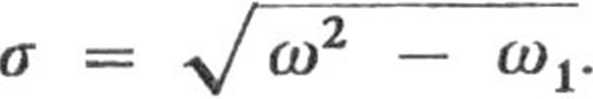
stąd

4

9

pr

y/ CD² —

O)

= 10 [kgnT*s *]

2.59.

a)

d²x

dt²

+

ln2 dx

5 dt

4- 4k²x = 0

b)    T = 1,006 [s].

c)    1,1 [W].

2.60. Równania ruchów drgających zapisujemy w postaci:

= x_a sin (cujt 4- a),

x₂ = x₀ sin (cu₂t 4- a).

Stąd ruch wypadkowy

cuj - m₂

2x₀ cos ---

t sm

cu_i 4~ cu 2

£ 4- a

przedstawia drganie harmoniczne, którego amplituda

A =

£

CU, — fUn

2a cos ---

2

zmienia się okresowo z częstością — co₂). Wobec tego okres dudnień

T =

2n

T.T

0)₁    - U>₂

T,

T,

93 [a]

2.61. Przyjmując kartezjański układ współrzędnych, możemy zapisać row nania drgań w postaci