img042 2

Przykład 3-19. Sporządzić wykresy V_x i M_a w belkach utwierdzonych jednostronnie, obciążonych jak na rys. 3-22a i d.

Siły poprzeczne:

-    belka wg rys. 3-22a

V?^B= -px,

_x = 0; V_A = 0, x = i, V_B = —pl,

-    belka wg rys. 3-22d

Vi^B = -P = -pl.

Wykresy sił poprzecznych pokazano na rys. 3-22b i e. Momenty zginające:

- belka wg rys. 3-22a:

2 '

px²

x = 0;    M_a = 0,

I    M    ^Pl2

x = /; M_B — ——, - belka wg rys. 3-22d:

= —Px— —plx,

x = 0; M_a — 0 x = l; M_B = —pl².

Wykresy M_a pokazano na rys. 3-22c i f. Z porównania tych wykresów wynika, że moment Mg od siły skupionej jest dwukrotnie większy od momentu M_B spowodowanego obciążeniem ciągłym, którego wypadkowa jest równa sile skupionej.

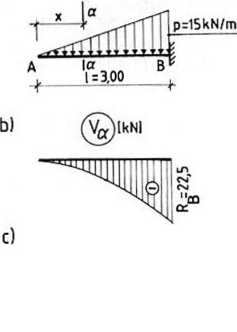
Przykład 3-20. Sporządzić wykresy V_a i M_a w belce utwierdzonej jednostronnie, obciążonej jak na rys. 3-23a.

Równanie siły poprzecznej

V? = - jP«x.

Rzędną obciążenia p_x wyznacza się z zależności

P_

l

px

X

skąd Px = —-

Po podstawieniu p_x do równania siły poprzecznej otrzymuje się:

x = 3 m; V_B = —22,5 kN. x = 0;    V_A = 0,

x = 1,5 m; K_a = 5,62kN,

Wykres V_a jest krzywą drugiego stopnia (rys. 3-23b). Z wykresu tego można odczytać wartość R„. Równanie momentu zginającego

1 px³

óT’

M, = ——p_xx—x

x = 0;    M_a = 0,

x = 1,5 m;    JW, = -2,81 kNm,

x = 3 m;    M„ = -22,5 kN-m.

Wykres M_a jest krzywą trzeciego stopnia (rys. 3-23c).

c) (PQ)lkNml

Tj

giiiiiiiiiLjiijy

o)

Rys. 3-22

a)

LH

CM~

CNI

2?

Rys. 3-23

ikN ml

Przykład 3-21. Sporządzić wykresy V_x i M_x w belce utwierdzonej jednostronnie, obciążonej jak na rys. 3-24a. Równania siły poprzecznej mają postać:

V?^c = 0,

V^C%^A — p(x—3),

* = 3 m;    v_c = 0,

^x = 5 m;    V_A = _30 kN.

ykres V_a przedstawiono na rys. 3-24b.

Momenty zginające wyznacza się z równań:

Alf = M = 10 kN ■ m,

2 Rys. 3-24