Kolendowicz41

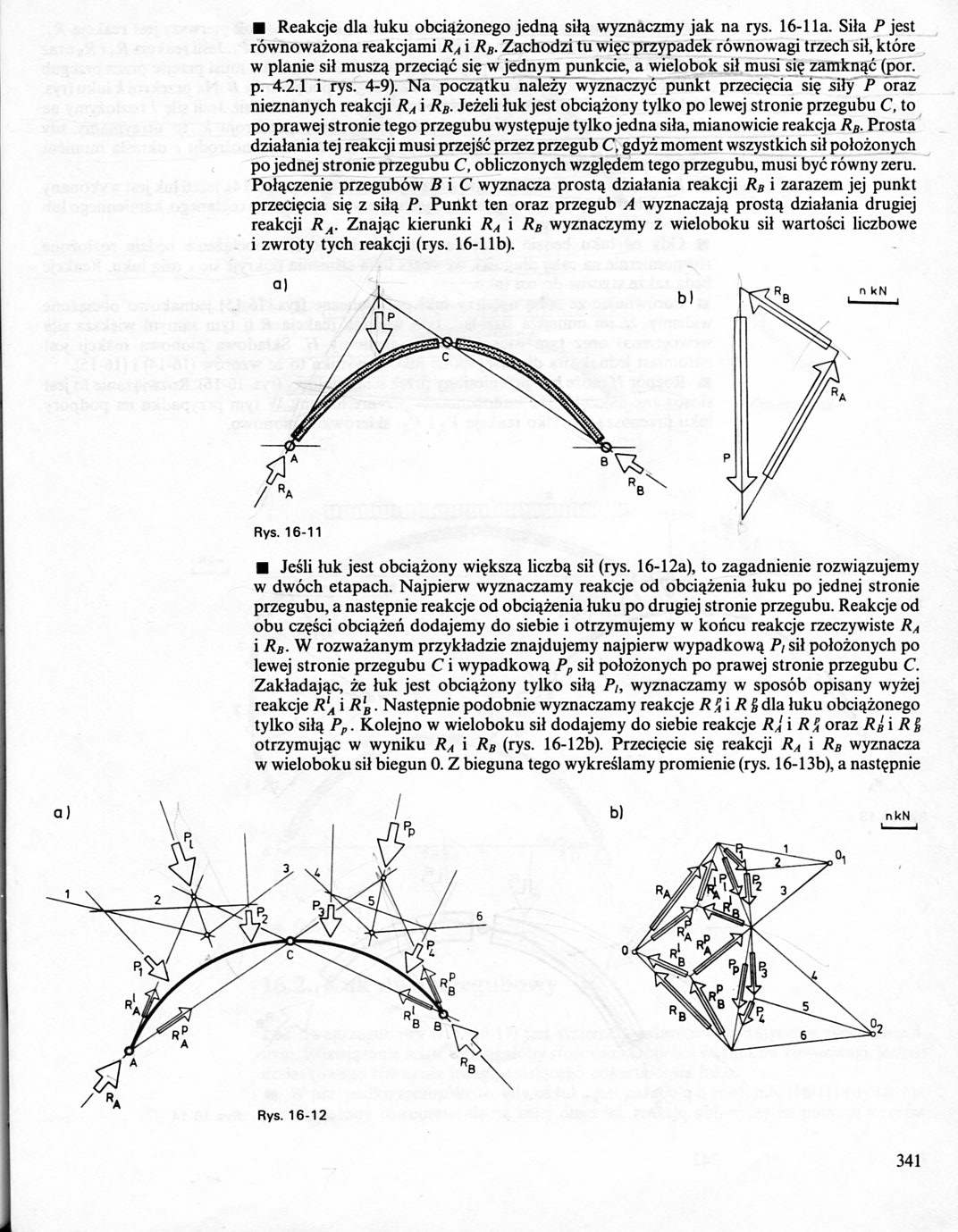
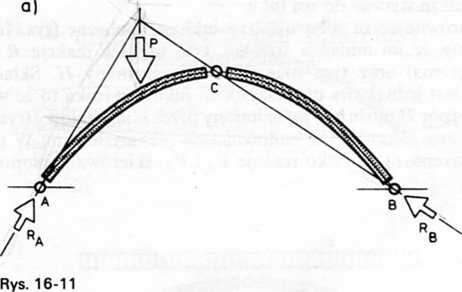
■ Reakcje dla luku obciążonego jedną siłą wyznaczmy jak na rys. 16-1 la. Siła Pjest równoważona reakcjami R_A i R_B. Zachodzi tu więc przypadek równowagi trzech sił, które w planie sił muszą przeciąć się w jednym punkcie, a wielobok sił musi się zamknąć (por. p. 4.2.1 i rys. 4-9). Na początku należy wyznaczyć punkt przecięcia się siły P oraz nieznanych reakcji R_A i R_B. Jeżeli łuk jest obciążony tylko po lewej stronie przegubu C, to po prawej stronie tego przegubu występuje tylko jedna siła, mianowicie reakcja R_B. Prosta działania tej reakcji musi przejść przez przegub C, gdyż moment wszystkich sił położonych po jednej stronie przegubu C, obliczonych względem tego przegubu, musi być równy zeru. Połączenie przegubów B i C wyznacza prostą działania reakcji R_B i zarazem jej punkt przecięcia się z siłą P. Punkt ten oraz przegub A wyznaczają prostą działania drugiej reakcji R_A. Znając kierunki R_A i R_B wyznaczymy z wieloboku sił wartości liczbowe i zwroty tych reakcji (rys. 16-1 lb).

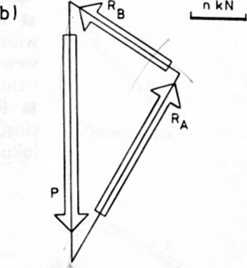
■ Jeśli łuk jest obciążony większą liczbą sił (rys. 16-12a), to zagadnienie rozwiązujemy w dwóch etapach. Najpierw wyznaczamy reakcje od obciążenia łuku po jednej stronie przegubu, a następnie reakcje od obciążenia łuku po drugiej stronie przegubu. Reakcje od obu części obciążeń dodajemy do siebie i otrzymujemy w końcu reakcje rzeczywiste R_A i R_b. W rozważanym przykładzie znajdujemy najpierw wypadkową P, sił położonych po lewej stronie przegubu C i wypadkową P_p sił położonych po prawej stronie przegubu C. Zakładając, że łuk jest obciążony tylko siłą P;, wyznaczamy w sposób opisany wyżej reakcje R‘_a i R‘_b . Następnie podobnie wyznaczamy reakcje R ^PA i R £ dla łuku obciążonego tylko siłą P_p. Kolejno w wieloboku sił dodajemy do siebie reakcje R_A i R J? oraz R_B i R § otrzymując w wyniku R_A i R_s (rys. 16-12b). Przecięcie się reakcji R_A i R_B wyznacza w wieloboku sił biegun 0. Z bieguna tego wykreślamy promienie (rys. 16-13b), a następnie

341