lastscan44

•    stopa efektywna jest tym większa, im częściej kapitalizuje się odsetki;

•    stopa efektywna jest największa przy kapitalizacji ciągłej.

Przykład 3.18

W przykładach 3.7-3.9 zajmowaliśmy się oprocentowaniem składanym o nominalnej stopie 24% z kilkoma wariantami kapitalizacji odsetek. Dla wszystkich wariantów obliczyliśmy roczny czynnik oprocentowujący, więc teraz - pomniejszając go o I - możemy natychmiast podać odpowiadające im stopy efektywne. Wyniki dotyczące omawianych przykładów zawiera tabela 3.7.

Stopa nominalna 24%
Kapitalizacja	Roczny czynnik oprocentowujący	Stopa efektywna (w %)
Roczna	1.2400	24,00
Półroczna	1,2544	25.44
Kwartalna	1,2625	26.25
Ciągła	1,2712	27.12

Wyniki przedstawione w tabeli 3.7 oraz na rysunku 3.6 potwierdzają sformułowane wyżej wnioski dotyczące stopy efektywnej, obliczonej dla tej samej

28% -r

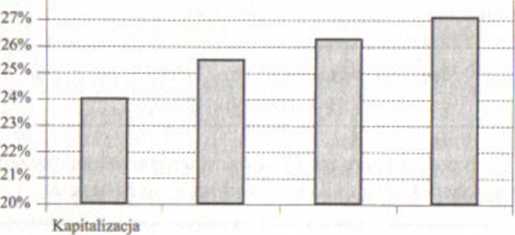
roczna    półroczna    kwartalna    ciągła

Ry&unck 3.6. Stopa efektywna pr/y stopie nominalnej 24%

stopy nominalnej i różnych okresów kapitalizacji. Jak widać, przy kapitalizacji rocznej stopa efektywna jest równa stopie nominalnej, stopa efektywna zwiększa się w miarę skracania okresu kapitalizacji i przyjmuje największą wartość pr/y kapitalizacji ciągłej.

■

Przykład 3.19

Stopy efektywne obliczone dla dwóch wariantów oprocentowania składanego (a) r_H m 9%, (b) r„ - 7%, pozwalają na wyciągnięcie wielu wniosków.

%

W każdym roku oprocentowanie (a) zwiększa wartość kapitału o 9%. entowanie (b) zaś o 7%.

•    Względny roczny przyrost wartości kapitału w przypadku (a) jest o 2 punkty entowe większy niż w przypadku (b).

•    Każda złotówka kapitału początkowego przyniesie po upływie roku odsetki nc 9 groszy w przypadku (a) i 7 groszy w przypadku (b).

•    Stosunek rocznych odsetek wygenerowanych przez ten sam kapitał w przy-ku (a) i (b) wynosi 9 : 7.

•    Jeśli stopy nominalne w przypadku (a) i (b) są równe, to w (a) odsetki egają częstszej kapitalizacji niż w (b).

•    Jeśli częstotliwość kapitalizacji odsetek w przypadku (a) i (b) jest jednakowa, [to w (a) stopa nominalna jest wyższa niż w (b).

3.7. Stopa zmienna w czasie, stopa przeciętna

Rozważania związane z oprocentowaniem składanym przy stopach zmieniają-

pch się w czasie rozpoczynamy od przypadku, gdy dla kolejnych laty = 1,2.....n

ine są stopy efektywne⁸    .....r^iH). Wiedząc, że roczny czynnik oprocen-

/ania w roku j wynosi 1 +/'¹, obliczamy wartość kapitału początkowego P po tywie kolejnych lat:

F, = />(l+/'^,)).

F₂ = P( l+/^i,,)(l+r'^2,)_ł F, = />(l+/^i,>)(l+^⁾)(l+0.

;z trudu można sprawdzić, że wartość kapitału po n latach jest dana wzorem

(3.45)

(3.46)

f = p nn+^j.

Jsetki na koniec roku n wynoszą oczywiście

/=/>[no+^)-n

y-1

wyższe równania (3.45M3.46) stanowią model oprocentowania rocznego »rzy stopie zmiennej w czasie. Sformułowany w punkcie 3.2 model oprocen-/ania rocznego przy stałej stopie r jest szczególnym przypadkiem powyższego ielu dla F¹ = r,j = 1.2, ...,n.

97

1

Dla uproszczenia zapuu pomijamy subskrypł .jcC. tradycyjnie stosowany w oznaczeniu stopy fektywnej.