matma0065

uscn £:■ ~~ e mej

U.interpretacje pierwszej pochodnej 71

fc- M

3 _

g) m = e^x ,

£j \ (w - l)³

i) /(w) =    —

w

3-U

k) f(x) = cos³ (x),

h) /(x) = 3x² e^_2x, j) g(P) = 4/7 ~² + 1, 1) d(m) = sin²(m³).

iitf w postsci funkcji złożonej f(x) =| i = x~ - 1, a funkcja zewnętrzr

■lii Obliczyć przyrost Ay wartości funkcji y = f(x) dla podanych przyrostów Ax argumentu x₀, jeśli:

a) y = -i-x², Xq = 2, x₀" = -1, Ax = 0,5, Ax = 0,1, Ax = -0,3 ,

L

2x =

\/x² + 1

pa »' renecie x₀ 6 (a, b) , to f jest

,1 jjran fałszywe. Jak wynika z punkaj : iŁ.: ::    punkcie x_Q = 0 (patrz

lim* zne ismieje /'(O)), gdyż//(O) -I

::n : - : ~ym punkcie x e D_f :

F

M(T] .

P® Hf-**    1 •

b i y =

2x - 1 3x + 2

, Xq = 1, Ax = 0,3 , Ax = 0,02, Ax = -0,2.

11.2. INTERPRETACJE PIERWSZEJ POCHODNEJ

Biech / oznacza funkcję różniczkowalną w punkcie x₀. Występujące w defi-

/(x₀ + h) -/(x₀)

■jii pochodnej wyrażenie ——-—i-— nazywamy ilorazem różnicowym funkcji

Iw punkcie x₀ dla przyrostu h. Zauważmy, że znak ilorazu różnicowego jest Hllitn:.: - gdy funkcja jest rosnąca; a ujemny - gdy funkcja jest malejąca w oto-HfeimiiiUL punktu x_Q. Zatem znak f (x₀) charakteryzuje monotoniczność funkcji / pzeniu punktu x₀. Iloraz różnicowy funkcji ma następującą interpretację metryczną. Przechodząca przez leżące na wykresie funkcji punkty p(x₀,f(x_Q)J, - Kf(x_Q + /*)) (patrz rys. II.2.1) linia prosta ma równanie:

f(^xo ⁺ h) -f(^xo)

y -fW =

(x-x₀).

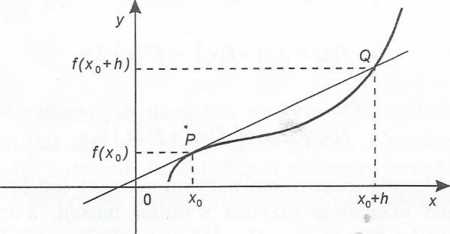
Rys. II.2.1