matma4

1 ₊ * x ₊ M ₊ ^{k(k iU} 2)v- ₊..., czyli ™

00 (lr\

• . ^ rozumiemy następująco: > x

to W

zwykłego symbolu Newtona. Colin Maclaurin 1698-1746 Szkocja.

2!

nie traktujemy jako

8.0bliczyć wskazane pochodne funkcji: a) /^(4l)(o), /⁽⁴²⁾(o) dla f(x) = xe^x b)/⁽⁴²⁾(l) dla /(x) = c)/^(30,(o) dla f(x) = ln(l + x²) d)/^(l0)(- 2) dla f(x) =

Wykorzystać: /^w(0) = a_n • n\, gdzie jest współczynnikiem w rozwinięciu funkcji f w szereg potęgowy. Jeżeli x₀ * O, to f^{n)(x_Q) = g^(w)(0), gdzie g(x) = f(x + x₀) czyli najpierw rozwijamy w szereg funkcję g(x) w punkcie x₀ = O.

0,5

9.0bliczyć przybliżoną wartość całki sumując pierwsze trzy wyrazy odpowiedniego szeregu: a) Jarctgx³dx

o

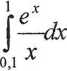
b)

Wykorzystać: funkcję podcałkową rozwijamy w szereg Maclaurina, a następnie całkujemy kolejne wyrazy tego rozwinięcia.

dx ⁰j*⁴ln(l + x)

lO.Obliczyć z dokładnością do 0,001 całki: a) Je ^v dx b) J ^arC^ dx c)    d) J--y —= e) J

0    0,5 ^X    z ^X    o yl + x 0,1

cosx

dx

x

6

Wykorzystać: funkcję podcałkową rozwijamy w szereg Maclaurina, a następnie całkujemy kolejne wyrazy tego rozwinięcia otrzymując pewien szereg liczbowy. Jeżeli jest on naprzemienny, to kolejne wyrazy bierzemy tak długo, aż trafimy na taki, którego wartość bezwzględna jest mniejsza od podanej dokładności. Gdy wszystkie jego wyrazy są dodatnie, to bierzemy ich tyle, aby suma wszystkich opuszczonych nie przekraczała podanej dokładności.

3