SWScan00076

im KosrmAxrr tlrmjsowe i opcjh

miUonn duluruw w jednym / Lr/ech następujących po sobie dni roboczych. Pierwszym dniem dostawy jest pierwszy dzień w miesiącu dostawy, w którym emitowane są 13-tygodniowe bony skarbowe. Do wyku pu dostarczanych rocznych bonów skarbowych musi wtedy pozostawać 13 tygodni. W praktyce oznacza to, że w momencie dostawy bony skarbowe mogą mieć 89, 90 lub 91 dni do wykupu.

Bony skarbowe są insfrutrittnlarni dyslamjttwymi (discounf instru• mena), co oznacza, że nic dają one żadnych płatności kuponowych, a inwestor otrzymuje w momencie wykupu wartość nominalną Ikiuu. Przed terminem realizacji kontraktu fuhtrts aktywami pierwotnymi są bony skarbowe, których okres do wykupu jest o 90 dni dłuższy niż czas pozostający do daty realizacji kontraktu. Jeśli na przykład dó terminu realizacji kontraktu pozostało 1Ó0 dni, to je^o .iktywarni pierwotnymi są 250-dniowc bony skarbowe.

Przyjmijmy dla potrzeb analizy, że lamin realizacji kontraktu na bony skarbowe jest równy T lat. a okres do wykupu bortów t>ędących aktywami pierwotnymi tego kontraktu upływa za "f lat (różnica pomiędzy T' i T jest równa 90 dni). Załóżmy następnie, że r i r oznaczają kapitalizowane w sposób ciągły wolne od ryzyka stopy procentowe dla okresów, odpowiednio, T i T laL Jeśli przyjmiemy, że wartość nominalna aktywów pierwotnych kontraktu (bonu skat Itowego) jest równa 100 dolarów, ich wartość bieżąca (V*) będzie wynosić:

V*-I00«r'^,r

Ponieważ bonv skarbowe nie przynoszą żadnych płatności kuponowych, można do nich zastosować wzór (3.5). z którego wynika, że cena terminowa iF) jest równa obecnej wartości aktywów pierwotnych pomnożonej przez er . ozyCt:

Fm 100* ^/JV -lOOe^ ^,v    (5.3>

Posługując się równaniem (5.1) powyższy wzór możemy przekształcić do postnei:

/•=100e'    ¹

gdzie r oznacza stupę terminową dla ukresu pomiędzy T i T" Wyrażenie powy/ji/jt: dowodzi, ż.e certa lurmiiiuwt bonów skarbowych to ceno. iaką osiągną one. jeżeli 90-dniowa stopa procentowa w dniu dustawy ladzie równa bieżącej stopie terminowej. Załóżmy, że V oznacza cenę bonów skarbowych o okresie do wykupu równym T, a zatem:

l'=l00c-^rr    (5.4)

Przy pomocy równania (53) można otrzymać inne wyrażenie opisujące /*’:

(5.5)

100^

Implikowana stopa rrpn

Stopa rrpo została już wspomniani! w rozdziale trzecim. Jest to stopa procentowa, według której inwestor rrur/.e pożyczyć środki sprzedając papiery wartościowe instytucji finansowej przy założeniu, żc odkupi je

Procentowe kontrakty futures

w terminie późniejszym. Jest u> jednocześnie stopa procentowa, według której instytucje finansowe mogą udzielać pożyczek wolnych o<l ryzyka. Stopa reno jest generalnie bardzo zbliżona do stopy rentowno lici l»onów skatbnwych. W celu sprawdzenia, czy istniej.) możliwości arbitrażowe na rynku bonów skarbowych. inwesioiTy często obliczaj;) implikowaną stopę repo (impłled repo ratę). Jest to stopa procentowa dla krótkoterminowych bonów skarbowych wynikająca z:

1.    cmy terminowej kontraktu na bony skarbowe, którego okres realizacji jest równy okresowi do wykupu krótkoterminowych bonów skarbowych:

2.    ceny bonów skarbowych o okresie do wykupu dłuższym o 90 dni niż dla krótkoterminowych bonów sluirbuwyuli.

Stosując dotychczasową notację, jest to T-letnia stopa procentowa określona przez V* i /*', a więc, korzystając z równania (5.5):

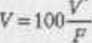
Pndsuiwiijąc tę zależność do równania (5.4) i rozwiązując je dla r można otrzymać implikowaną stopę r«»po w waninkadi kapitalizacji ciągłej;

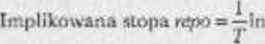
(f)

JcAli rentowność bonów skarbowych o okresie do wykupu równym T różni się od wartości wynikającej z powyższego wzorj. to istnieje możliwość zawarcia trawa kej i arbitrażowej.

Arbitraż oparty na Implikowanej stopie repo

Możliwości arbitrażowe /.ilustrujemy przykładem, w którym bieżąca cena nabycia bonów skarbowych o okresie du wykupu równym 146 cni (na 100 dolarów wartości nominalnej) jest równa 95,21 dolara, a terminowa cena nabycia 90-dr.iowych bonów skarbowych dla kontraktów fiiMm o terminie realizacji upływającym za 56 dni wynosi 96.95 dolara. W naszym przykładzie T = 56/165 = OJ 5.14, a implikowana stopa repo jest równa:

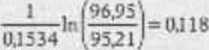
czyli 11.8 procent w skali rocznej przy założeniu kapitalizacji ciągłej.

Jeśli 56*dniow» stop* rentowności bonów skarbowych jest niższa niż 11.8 procent w skali rocznej, inwestor może:

1.    wykorzystując transakcję repo pożyczyć środki (według stopy rentowności bonów skarbowych) na 56 dni;

2.    zająć pozycję krótką w kontrakcie fuiwts',

3.    kupić 146-dniowe bom¹ skarbowe.