mech2 155

308

Z ogólnych wyrażeń na rzuty wektora krętu

308

otrzymamy

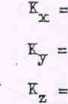
U) -	i	Cl3_ —	I	U)
X	xy	7	xz	Z
e V) i	^ryz	“z "	■^yz	^ux
to„ ~	i	to -	I	UJ
z	zx	X	zy	7
H* II	■^xx	to,

^Ky “ -¹yx"'

Równania analityczne zasady pędu przyjmą postać:

⁰ = ^Sx ^{+ S}1x ^{+ S}2x*

^{0 = s}y ^{+ s<}iy ^{+ s}2y>

-®y_c (»- 03_o) = s_z + s_1z + s_2z.

Równania analibyozne zasady krętu przyjmą postać:-

^Jxx ^Cu) - “o) = ^Sz ^b’

"V ^(uj “ ^(JJo⁾ = - ^S1z ^{r + S}z^R’

-^Jzx ^(uł - “o^ = -^S1y ^r-

Żądamy w zadaniu, by punkt M był środkiem uderzeń,co oznaoza.że i S₂

muszą być równe zeru. Poprzednio podane równania zasady pędu i zasady

krętu będą więc następujące: S =0, S = 0.

x    y

-my₀ (oj - u₀) = S_z,    (1)

( U) - w₀) = -S_zb ,    (2)

(3)

-1^ Cm - u>₀) = S_za,

—X (u) — u) ) = 0.

zx ^v o

Wynika z tego, że impulB S musi być skierowany prostopadle do płaszczyzny tarjzy oraz, że moment dewiacji I „ musi być równy zeru (co jest dla tarczy spełnione tożsamościowo).

509

Z równań (1) (2) (3) możemy wyznaczyć wzory na współrzędne środka uderzeń:

I

a =    ,

b = ia .

® 7n

Przystępujemy do obliozeń dla rozpatrywanej ćwiartki koła (rys. 229b)

m = -J- n r² p ,

przy ozyo p — gęstość powierzchniowa,

t y

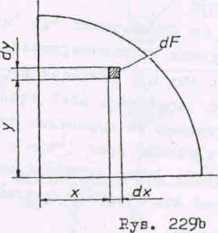
\y

Rys. 2?0

Y _ -ii—— (dla ćwiartki tak jak dla półkola)

•'o    5 n

2    4

t    1 „ r nr

^Z~ = TT ® TT = =16" P’

V?^:

I^y = J xydm = p j J xydydx =

m    o o

= p J    x -—** = P T (j² j    ^xdx - J    x^dx j)    = P TT •

o    ^ o    o ^

r⁴

PT

Podstawiająo wyznaczone wielkośoi do wzorów na współrzędne a i b trzymamy

= i *•

-5h-

ny,

O 'l „,2,, 4 ^r

TT nr P - _T

\

ii