mechanika28

Rozwiązanie Sprawdzenie GN, SW:

Układ jest równoważny trzem tarczom połączonym przegubowo. Przeguby tworzy trójkąt. Każ.dy przegub jest równoważny dwóm więzom elementarnym, stąd:

e ■ 6, t - 2, e - 3f => GN (1 zasada), SW

Powyższy zapis wyrażamy słownie następująco: w układzie występuje 6 ele mentamych więzów i 2 tarcze (nie licząc tarczy ostoi), a więc jest spełniony warunek e - 3f, czyli układ jest geometrycznie niezmienny według I zasady i statycznie wyznaczalny.

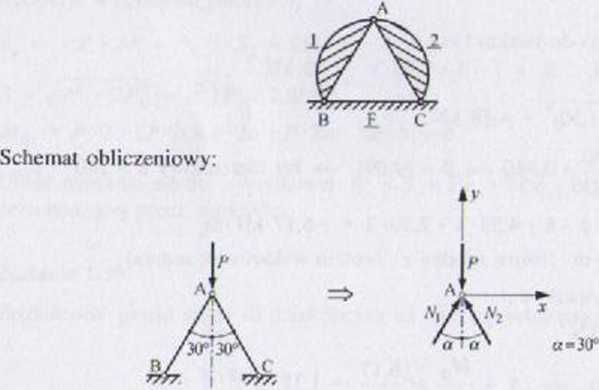
Aby wyznaczyć siły w prętach AB, AC. wystarczy rozważyć równowagę węzła A. Myślowo przecinamy pręty w węźle A i ujawniamy siły w prętach. Założono ściskanie prętów. Tworzy się płaski zbieżny układ sił. spełniający 2RRS:

£

£

X = 0:

Y = 0:

= ^P

2cosa

N_x sin a - N₂ sin a = 0 =*

N, cos a + N₂ cos a - P = 0 => 2/V, cos a = P |: (2 cos a)

= - ^P — =    - —P*0.577P = 0,577-200 = 1154 N

2 cos 30    ₂-j3 fi

N₂ = 1154 N

Układ spełnia warunek symetrii względem osi y. Dodatnie wartości N_t, N. świadczą o trafności założenia ściskania prętów.

56

Smyka I 2.2. Wy/naczank* reakcji w układach płaskich

/ "I MMC 1.12

|nyiiiK’/yć siły vv prętach układu obciążonego siłą P = 2000 N

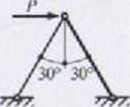
wiązanie

Hpt.iwdzenie GN. SW — jak w zadaniu 1.11. li In-mat obliczeniowy:

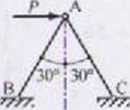
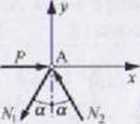
nr-30*

Mo/patrujemy równowagę węzła A. Przyjęto rozciąganie pręta AB i ściskanie prę la AC.

‘IłRS płaskiego zbieżnego układ sił:

) X - 0: P - sina - N₂ sin a * 0 \ Y = 0:    -N_x cos a + N₂ cos o = 0 =» N₂ - N,

= P = 2000 N

/’ .V, sin a N, sin a = 0 =* 2N_y sin a = P |: 2 sin a P    P P2

21

2 sin a    2 sin 30°

P - 2000 N

/.ulanie 1.13

2000 N.

\S s znaczyć siły w prętach układu obciążonego siłą P

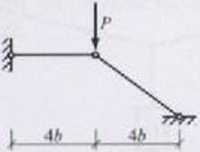
57

Si utyka I 2 2, Wyznaczanie reakcji w układne h płaskich