mechanika35

Rozwiązanie

Sprawdzenie GN. SW — jak w zadaniu 1.22. Schemat obliczeniowy:

"e,		l"		"h,	I^3' <i	f2
	B				D
	a_	__£_	22*		A C	2 P
	»A			J	«x "^c |»ć —^h—J-—4—ł—6—i.

P. = P-cos 60° = -P, P, = P* sin 60° - &P ¹ 2 ² 2

Obliczenie składowych sil ukośnych:

H_c = R_c-sin 30° = ¹ K_c = P_c*cos30° = -^P_c 2 2

3RRS płaskiego układu sił:

Y.^x *o=	//b^c + Pi-2P =	0		(1)
M II O	^*Kc-3i>-/>2 =	0		(2)
5>b *0:	Hc-b + Vc2b 3P*	6 P2	■3b-2P b = 0 |:*	(M
	2P-ip 2
			Hb+0J5Rc = W
		=* '	Ka ♦ 0t866Pr - 3.866P
Ij^2-j5 2 v 2	/Ł. = 5P ♦ 3 - ^ P ^ 2		2,232/^ = 7,598P
(3) =* Pr =	^7'^598 P - 3.404P
	2,232
(1) => //B =	UP-0,5/^ = 1,5P	” 0,5	3.404P = -0,202P
(2) -» Ka =	3.866P 0,866Pc =	3,866P - 0.866 • 3.404P 0,918P

Statyku. 1.2.2. Wyznaczanie rcukcjt w układach płmkkh

70

l kontrolny:

|.4ton -nona warunku kontrolnego wynosi:

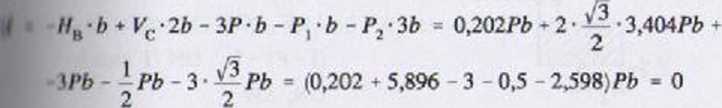
V • 'f (lewa strona równa się prawej stronie).

• M,. V_K = 0,918/* (ściskanie).

//,, ■    0,202P (rozciąganie),

K, - 3,404/* (ściskanie).

|i«u. nttirz: W przypadku trudniejszego zadania (duża liczba operacji) wskaza-1 |Pm sprawdzenie obliczeń. Warunek kontrolny zapisujemy w postaci sumy htkuitów względem innego niż w równaniu (3) punktu. W obliczeniach nitowano dokładność 3 cyfry po przecinku. W wyniku obliczenia można ulw mi ■ otrzymać

4    0,001 Pb lub <£ = -0,001 Pb

•»• i> i /wiązane z dokładnością obliczeń. Wówczas piszemy

4    0,001 Pb * 0 lub ££ = -0,001 Pb * 0

t ••kinie 1.24

■WiMLzyć reakcje w więzach łączących tarcze ze sobą i z ostoją:

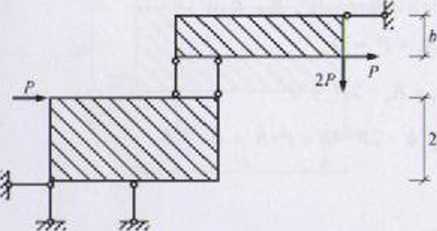
2 b

+ 26-jA.p..j-2*-\

71

tk.i I 2,2 Wy/nac/.anie reakcji w układach płaskich